When a body has an increase in temperature, the molecules that make it up receive energy and become agitated, causing an increase in the dimensions of the object. This phenomenon is known as thermal expansion. Similarly, when a body is cooled, its energy decreases and so does molecular agitation, causing a reduction in its dimensions, which is known as contraction thermal.
THE thermal expansion can be classified in three ways: linear, shallow and volumetric.
linear thermal dilation
when the temperature variation of a body to change the distance between two points, the linear thermal expansion, which can be a variation in the length of a bar, the radius of a sphere, the diagonal of a cube or a square, among others.
As an example, consider an iron bar of length L0 with initial temperature Ti. By raising your temperature to Tf , the length will be increased to L. Look at the picture:

Diagram showing linear thermal expansion caused by temperature rise
The temperature variation (ΔT) is the difference between the final and initial temperature:
ΔT = Tf - Ti
The linear thermal expansion (ΔL) produced by this temperature variation is the difference between the final length L and the initial length L0:
Δ L = L - L0
This expansion suffered by the bar is proportional to the temperature variation and the initial length of the bar, so it can also be calculated with the Law of Linear Thermal Dilation by the formula:
Δ L = α. L0. Δ T
The proportionality constant α is called linear thermal expansion coefficient of the material that makes up the bar. Its unit of measurement is the reciprocal degree Celsius, being represented by ºC -1. This quantity assumes a different value for each type of material, representing the linear thermal expansion for each unit of length and for each unit of temperature variation.
Do not stop now... There's more after the advertising ;)
See the following table for the values of the coefficient of linear thermal expansion of some substances:
Substance |
Coefficient (10-6 °C -1) |
Lead |
27 |
Aluminum |
25 |
Silver |
20 |
Silicon |
2,6 |
Steel |
14 |
Gold |
15 |
Graphic representation of linear thermal expansion
We can obtain linear thermal expansion from a graph of length versus temperature:
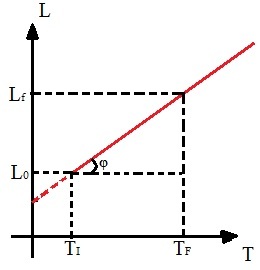
Graph of length versus temperature of linear thermal expansion
We can relate the angle φ to the Law of linear thermal expansion, since:
Δ L = α. L0. Δ T
and
ΔL = α. L0
Δ T
being the straight line angular coefficient which represents the variation in length with temperature, it is given by:
tg φ = ΔL
Δ T
soon:
tg φ = α. L0
The line cannot pass through point 0, since the initial length cannot be equal to zero.
One of the consequences of linear thermal expansion can be seen in engineering works, for example, the expansion joints (figure in the title) that exist on train tracks or sidewalks. They are simply a small empty space left in parts of the construction for the expansion caused by the temperature variations, such as in the case of a fire or even natural variations, do not damage the structure of the buildings. If these expansion joints did not exist, any rise in temperature could cause the concrete or hardware to bend or break.
By Mariane Mendes
Graduated in Physics
Would you like to reference this text in a school or academic work? Look:
TEIXEIRA, Mariane Mendes. "What is linear thermal expansion?"; Brazil School. Available in: https://brasilescola.uol.com.br/o-que-e/fisica/o-que-e-dilatacao-termica-linear.htm. Accessed on June 28, 2021.