A matrix is triangular when elements above the main diagonal or elements below the main diagonal are all null. There are two possible classifications for this type of matrix: the first is when the elements above the main diagonal are null, which sets up a lower triangular matrix; the second is when the elements below the main diagonal are null, setting up an upper triangular matrix.
To calculate the determinant of a triangular matrix by Sarrus' rule, just perform the main diagonal multiplication, since the other multiplications will all be equal to zero.
Read too: Array — what it is and existing types

Triangular Matrix Types
To understand what a triangular matrix is, it is important to remember what the main diagonal of a square matrix is, which is the matrix that has the same number of rows and columns. The main diagonal of the matrix is the terms a.ij, where i = j, that is, they are the terms in which the row number is equal to the column number.
Example:

Understanding what a square matrix is and what its main diagonal is, let's know what a triangular matrix is and its classifications. There are two possible classifications for the triangular matrix: Thelower triangular matrix and upper triangular matrix.
- Lower triangular matrix: occurs when all terms above the main diagonal are equal to zero and the terms below the main diagonal are real numbers.

Numerical example:

- Upper triangular matrix: occurs when all terms below the main diagonal are equal to zero and the terms above the main diagonal are real numbers.
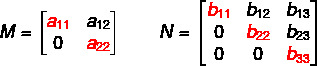
Numerical example:
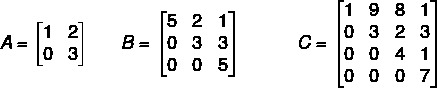
diagonal matrix
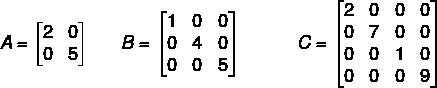
The diagonal matrix is a particular case of triangular matrix. In it, the only terms that are nonzero are those that are contained in the main diagonal. The terms above or below the main diagonal are all equal to zero.

Numerical examples of diagonal matrix:
Determinant of a triangular matrix
Given a triangular matrix, when calculating the determinant of this matrix by Sarrus' rule, you can see that all multiplications are equal to zero, except the multiplication of the term of the main diagonal.

det (A) = a11 · a22· a33 + the12 · a23 · 0 + the13 · 0 · 0 - ( The13 ·The23 ·0 + the11 · a23 · 0 + the12 · 0· a33)
Note that in all terms except the first, zero is one of the factors, and all multiplication by zero is equal to zero, so:
det (A) = a11 · a22· a33
Note that this is the product between the terms of the main diagonal.
Regardless of the number of rows and columns a triangular matrix has, its determinant will always be equal to the product of the terms of the main diagonal.
See too: Determinant — feature applied to square matrices
Triangular Matrix Properties
The triangular matrix has some specific properties.
- 1st property: the determinant of a triangular matrix is equal to the product of the terms of the main diagonal.
- 2nd property: the product between two triangular matrices is a triangular matrix.
- 3rd property: if one of the terms of the main diagonal of the triangular matrix is equal to zero, then its determinant will be equal to zero and, consequently, it will not be invertible.
- 4th property: the inverse matrix of a triangular matrix is also a triangular matrix.
- 5th property: the sum of two upper triangular matrices is an upper triangular matrix; similarly, the sum of two lower triangular matrices is a lower triangular matrix.
solved exercises
1) Given the matrix A, the value of the determinant of A is:

a) 2
b) 0
c) 9
d) 45
e) 25
Resolution
Alternative d.
This matrix is lower triangular, so its determinant is the multiplication of terms on the main diagonal.
det (A) = 1·3·3·1·5 = 45
2) Judge the following statements.
I → Every square matrix is triangular.
II → The sum of an upper triangular matrix with a lower triangular matrix is always a triangular matrix.
III → Every diagonal identity matrix is a triangular matrix.
The correct order is:
a) V, V, V.
b) F, F, F.
c) F, V, F.
d) F, F, V.
e) V, V, F.
Resolution
Alternative d.
I → False, because every triangular matrix is square, but not every square matrix is triangular.
II → False, as the sum between an upper and lower triangular matrix does not always result in a triangular matrix.
III → True, as the terms different from the diagonal are equal to zero.
By Raul Rodrigues de Oliveira
Maths teacher
Source: Brazil School - https://brasilescola.uol.com.br/matematica/matriz-triangular.htm
