In operations between matrices, we know that matrix multiplication is a long and laborious process. Thus, today we will know a theorem that avoids having to find the product-matrix to calculate its determinant, and in which the determinant of each matrix can be used separately.
For this, we will state Binet's theorem and see how it is applied in the calculation of determinants.
“Let A and B be two square matrices of the same order and AB the product matrix, thus we have that det (AB)=(det A).(det B).”
That is, instead of finding the matrix-product and then calculating its determinant, it is possible to calculate the determinant of each matrix and multiply them.
Let's look at an example to understand how hard the work would be if Binet's theorem did not exist.
Example 1:
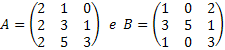
If we didn't have Binet's theorem, we would have to do the following process to calculate det (A.B).
1. Find the product-matrix (A.B).
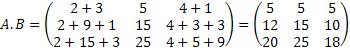
2. Calculate the determinant of the matrix-product.

If you didn't have a calculator to do these multiplications with big numbers, it would be complicated, wouldn't it?
See the calculation of the same determinant, but using Binet's theorem.
First let's find the determinant of each matrix, separately:
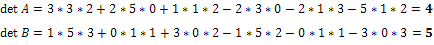
As we have seen, by Binet's theorem, det(AB)=(det A).(det B):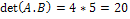
Example 2:
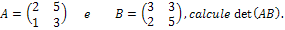
We will do the calculations again using the two procedures:

It is really a much easier and more practical process compared to the previous one, after all it saves the work of having to find the matrix-product, which is a long and laborious process. In addition, the matrix-product determinant most often has a product of large numbers, which entails a laborious multiplication and addition calculation of several numbers.
By Gabriel Alessandro de Oliveira
Graduated in Mathematics
Brazil School Team
Matrix and determinant- Math - Brazil School
Source: Brazil School - https://brasilescola.uol.com.br/matematica/teorema-binet.htm
