THE conservationgivesenergymechanics is one of the laws of mechanics that stem from principleinconservationgivesenergy. According to the law of conservation of mechanical energy, when none dissipative force acts on a body, all its energy related to movement is kept constant. This is equivalent to saying that the kinetic energy and the energypotential of the body never change.
Understanding the law of conservation of mechanical energy is essential for solving a large number of situations in Physics that approach ideal situations, so this is one of the most demanded issues in the field gives Mechanics in Enem tests.
See too: Traction - understand this other physical concept studied by Mechanics
What is mechanical energy conservation?
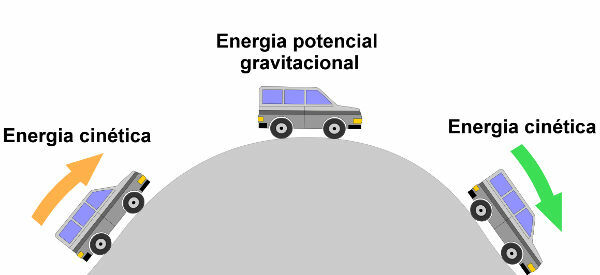
THE conservationgivesenergymechanics states that all the energy related to the movement of a body is kept constant when no dissipative forces, such as friction and drag forces, act on it.
When we say that mechanical energy is conserved, this means that the sum of the
energykinetics with the potential energyis the same at all times and in any position. In other words, no portion of the mechanical energy of a system is transformed into other forms of energy, such as Thermal energy.Given the above, according to the law of conservation of mechanical energy, in a non-dissipative system, we can say that the mechanical energies in two distinct positions are equal.

ANDM – mechanical energy
ANDÇ - kinetic energy
ANDP - potential energy
In order for us to better understand the concept of conservation of mechanical energy, it is necessary to know what it is energykinetics and energypotential, so we will briefly explain each of these concepts in the following topics.
Kinetic energy
THE energykinetics is the energy contained in any body that has a amount of movement not null, that is, as long as the body has pasta and velocity, it will be endowed with a certain amount of kinetic energy.
THE energykinetics is scalar greatness whose unit, according to the ssystem IInternational Units, and the joule (J). The kinetic energy formula states that this energy is equal to the product of the pasta (m) and the squaregivesvelocity (v²) divided by 2.

m - pasta
v - velocity
ANDÇ - kinetic energy
To learn more about this form of energy, visit our specific article: Kinetic energy.
Potential energy
THE energypotential it is a form of energy that can be stored and that depends directly on the position where a body is in relation to some field of strength, such as the gravitational field, electric field and magnetic field.
THE energypotential can only be accumulated in a body when it is subject to the action of a strengthconservative, that is, a force that always applies the same amount of energy to a body, regardless of the path taken.
An example of conservative force is the strength Weight: if a body is lifted against the action of the weight force from the ground to a certain height, regardless of the trajectory traveled by this body, the potential energy gain will depend exclusively on the difference between the two heights.
When it comes to exercises on the conservation of mechanical energy, there are two more common types of potential energy: a gravitational potential energy and the elastic potential energy. Gravitational potential energy is the form of energy relative to the height of a body relative to the ground. It depends on the body mass, on the gravity acceleration in place and at the height

g – gravity (m/s²)
H – height (m)
THEelastic potential energyis the one related to deformation of some object, like a rubber band. To calculate it, one takes into account how much the object was deformed (x), as well as the constantelastic of this object (k), measured in newtonpersubway. If an object has an elastic constant of 800 N/m, this indicates that, to be deformed by one meter, this object is acted upon by a force of 800 N. The formula used to calculate the elastic potential energy is as follows:

To learn more about this form of energy, visit our specific article: Energy potential.
mechanical energy
THE mechanical energy and the sum of kinetic and potential energy. In other words, it is all energy that is related to the movement of a body. The formula for mechanical energy is as follows:
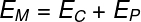
Mechanical energy conservation formula
The formula for the conservation of mechanical energy is such that the sum of kinetic energy and potential energy is equal for any points in a mechanical system where no dissipative forces act.
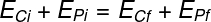
ANDCi and isCf -final and initial kinetic energy
ANDCi and isFederal Police -final and initial kinetic energy
Although the above formula is general and can be applied in any case where mechanical energy if conserved, it is necessary to emphasize that each case can present a different form of energy potential. Thus, solving exercises is the best way to understand the different cases.
Read too:Free fall - better understand this movement where there is no friction force
Solved exercises on the conservation of mechanical energy
Question 1 - A body with mass m = 2.0 kg rests against a spring with an elastic constant equal to 5000 N/m, compressed by 2 cm (0.02 m). Neglecting the dissipative forces and based on the figure, determine the height reached by the body after the spring is released and mark the correct alternative.
(Data: g = 10 m/s²)
a) 4 cm
b) 10 cm
c) 5 cm
d) 20 cm
e) 2 cm
Template: letter C.
Resolution:
To solve the exercise, it is necessary to apply the law of conservation of mechanical energy. In this sense, we see that the initial mechanical energy is purely elastic potential, and the final mechanical energy is purely gravitational potential. In this way, we must make the following calculation:

Based on the developed calculation, we find that the body rises to a maximum height of 5 cm, so the correct alternative is the letter C.
Question 2 - A body is released from the rest of a ramp at a height of 4 m. Determine the speed at which the body will be when it is 2 m above the ground and indicate the correct alternative.
a) 2√10 m/s
b) 20 m/s
c) 4√10 m/s
d) 2√5 m/s
e) 3√2 m/s
Template: letter a.
Resolution:
We must apply the law of conservation of mechanical energy at the highest points and at the point of height equal to 2 m. To do this correctly, we need to remember that, at the highest point, the body was at rest, so all its mechanical energy was expressed in the form of gravitational potential energy. At the point where the height is equal to 2 m, there is so much energypotentialgravitationalhow muchenergykinetics. Note the calculation in the following figure:

At the end of the above calculation, when we calculated the square root of 40, we factored the number so that the result yielded 2√10, so the correct alternative is the letter A.
By Rafael Hellerbrock
Physics teacher
Source: Brazil School - https://brasilescola.uol.com.br/fisica/principio-conservacao-energia-mecanica.htm

