One-vector norm is another name given to modulus of a vector. To understand the concept of a vector's modulus or norm, it is important to first understand the concept of modulus of a real number, as both refer to the same procedure, but with calculations many different.
There is a correspondence between the real numbers and the number line called bi-univocal. This means that each point on the number line represents a real number and each real number represents a point on the number line. Also, this line is ordered, that is, the numbers are arranged in it ascending from right to left.
These two features of the number line allow distances between real numbers to be calculated. Therefore, the magnitude between two real numbers x and y is defined as the absolute value of the difference between x and y and is denoted by |x – y|. Thus, the module represents the distancebetween two numbers reals on the number line.

Module between real numbers - 2 and + 4
Note that the definition above is for the modulus between two real numbers. When it comes to the magnitude of a real number, it refers to the distance between that number and 0 (zero), which is the origin of the number line. Therefore, |x| is the distance between point x and point 0 on a number line.
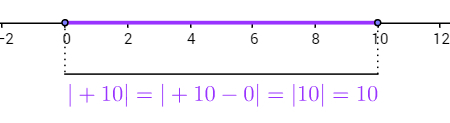
Real number module +10
In relation to vectors, they are mathematical objects defined in any type of space, be it a straight line, a plane or spaces with many dimensions. In addition, they are oriented straight lines created to describe straight movements and are marked with direction, direction and intensity. Since these are straight segments first of all, it is possible to measure their length using calculations that involve distance between two points.
One-vector norm
→ First case:
Taking the plane as an example, generally, vectors are represented starting at point O = (0,0) and ending at point A = (x, y). If this is the case for vector v, we can write that vector v = (x, y). In that case, to calculate the modulus of vector v, also called standard, just calculate its length, obtained from the distance between points A and O.
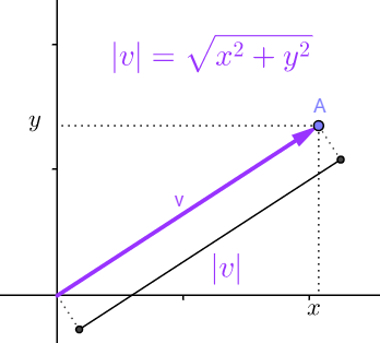
Distance from A to O in the plane
→ Second case:
Taking the plane as an example, a vector could have been taken anywhere on that plane. Therefore, considering that vector v starts at point G = (a, b) and ends at point L = (c, d), the norm of this vector can be obtained in two ways:
1 – transporting the vector, without any rotation or dilation, to the origin of the plane and repeating the previous procedure.
2 – Calculating the distance between L and G.
This last case is given by the following expression:

Expression used to calculate the norm of any vector in the plane
By Luiz Paulo Moreira
Graduated in Mathematics
Source: Brazil School - https://brasilescola.uol.com.br/matematica/norma-um-vetor.htm


