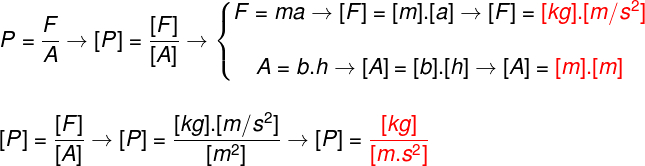We know that lenses are constantly inserted in our daily lives, for example, in glasses, cameras and various optical instruments. Thus, we can define spherical lenses as being any optical system consisting of three homogeneous and transparent media.
The positions and heights of the object and its respective image are determined using the same equations already studied in spherical mirrors. Thus, in a similar way to the procedure adopted in spherical mirrors, the transversal linear increase equation can be determined based on similarity relationships of triangles, in the process of image formation by the lenses.
Let's look at the figure above: it shows us a linear object MN and its corresponding image MONO, both transversal in relation to the main axis, for a thin spherical lens, obtained from the graphic method.
Do not stop now... There's more after the advertising ;)
The highlighted triangles MNO and MONO are similar triangles. So we have:
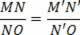
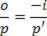

By definition, the relationship

is the transverse linear increase, or magnification. Therefore, we have:

By Domitiano Marques
Graduated in Physics
Would you like to reference this text in a school or academic work? Look:
SILVA, Domitiano Correa Marques da. "Transverse linear increase"; Brazil School. Available in: https://brasilescola.uol.com.br/fisica/aumento-linear-transversal.htm. Accessed on June 28, 2021.