Equation: what is it, basic concepts, types, examples

One equation is a mathematical sentence that has an equality and at least one unknown, that is, when we have the involvement of a algebraic expression and an equality. The study of equations requires prior knowledge, such as the study of numeric expressions. The purpose of an equation is find the unknown value that turns equality into an identity, that is, a true equality.

Read too:Operations with fractions – how to calculate?

Basic Concepts for Equation Study

An equation is a mathematical sentence that has a unknown, at least, and a equality, and we can rank it by its number of unknowns. See some examples:

a) 5t – 9 = 16

The equation has an unknown, represented by the letter t.

b) 5x + 6y = 1

The equation has two unknowns, represented by the letters x and y.

c) t⁴ – 8z = x

The equation has three unknowns, represented by the letters ok,z and x.

Whatever the equation, we must take into account your universe set,composed of all the possible values ​​that we can assign to the unknown, this set is represented by the letter U.

• Example 1

Consider the equation x + 1 = 0 and its possible solution x = –1. Now consider that the universe set of the equation are the natural.

Note that the supposed solution does not belong to the universe set, since its elements are all the possible values ​​that the unknown can take, so x = –1 is not the solution to the equation.

Of course, the greater the number of unknowns, the more difficult it is to determine your solution. THE solution or source of an equation is the set of all the values ​​that, when assigned to the unknown, make the equality true.

• Example 2

Consider the equation with an unknown 5x – 9 = 16, verify that x = 5 is the solution or root of the equation.

So that it is possible to say that x = 5 is the solution of the equation, we must substitute that value in the expression, if we find a true equality, the number will be the tested solution.

5x – 9 = 16

5(5) – 9 = 16

25 – 9 = 16

16 = 16

See that the equality found is true, so we have an identity and the number 5 is a solution. So we can say that the solution set is given by:

S = {5}

• Example 3

Consider equation t² = 4 and check whether t = 2 or t = –2 are solutions to the equation.

Analogously, we should substitute the value of t into the equation, however, note that we have two values ​​for the unknown and therefore we should perform the verification in two steps.

Step 1 – For t = 2

t²= 4

2² = 4

4 = 4

Step 2 – For t = –2

t² = 4

(–2)² = 4

4 = 4

See for t = 2 and t = – 2 we find an identity, so these two values ​​are solutions to the equation. Thus, we can say that the solution set is:

S = {2, –2}

Equation Types

We can also classify an equation as to the position that the unknowns occupy. See the main types:

• Polynomial Equations

At polynomial equations are characterized by having a polynomial equal to zero. See some examples:

The) 6t³+ 5t²–5t = 0

The numbers6, 5 and –5 are the coefficients of the equation.

B) 9x – 9= 0

The numbers 9 and – 9 are the coefficients of the equation.

c) y²– y – 1 = 0

The numbers 1, – 1 and – 1 are the coefficients of the equation.

• Equation degrees

Polynomial equations can be classified by their degree. As well as the polynomials, the degree of a polynomial equation is given by highest power that has a non-zero coefficient.

From the previous examples a, b and c, we have that the degrees of the equations are:

a) 6t³ + 5t² –5t = 0 → Polynomial Equation of third degree

b) 9x – 9 = 0 → Polynomial Equation of first degree

ç) y² – y – 1 = 0 → Polynomial Equation of high school

Read too: quadratic equationu: how to calculate, types, examples

• rational equations

Rational equations are characterized by having their unknowns in the denominator of a fraction. See some examples:

Read too: What are rational numbers?

• irrational equations

At irrational equations are characterized by having their unknowns inside an nth root, that is, inside a radical that has index n. See some examples:

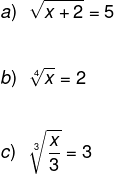
• exponential equations

At exponential equations have the unknowns located in the exponent of a potency. See some examples:

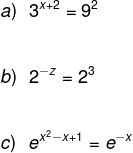
• logarithmic equation

At logarithmic equations are characterized by having one or more unknowns in some part of the logarithm. We will see that, when applying the definition of the logarithm, the equation falls in some of the previous cases. See some examples:

See too: First degree equation with an unknown

How to solve an equation?

To solve an equation, we must study the methods used in each type, that is, for each type of equation, there is a different method to determine the possible roots. However all these methods are derived from the equivalence principle, with it it is possible to solve the main types of equations.

• Equivalence principle

Second principle of equivalence, we can freely operate on one side of an equality as long as we do the same on the other side of the equality. To improve understanding, we will name these sides.

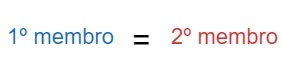
Therefore, the equivalence principle states that it is possible operate on the first limb freely as long as the same operation is done on the second member.

In order to verify the equivalence principle, consider the following equality:

5 = 5

Let's go now to add on both sides the number 7, and note that the equality will still be true:

5 =5

5 + 7= 5 + 7

12 = 12

Let's go now subtract 10 on both sides of the equality, note again that the equality will still be true:

12 = 12

12 – 10 = 12 – 10

2 = 2

see that we can multiply or share and raise to a potency or even extract a source,as long as it is done on the first and second member, the equality will always hold true.

To solve an equation, we must use this principle together with the knowledge of the operations mentioned. In order to facilitate the development of the equations, let's omit the operation done on the first member, it is equivalent to saying that we are passing the number to the other member, exchanging the sign for the opposite.

The idea to determine the solution of an equation is always isolate the unknown using the equivalence principle, Look:

• Example 4

Using the equivalence principle, determine the solution set of the equation 2x – 4 = 8 knowing that the universe set is given by: U = ℝ.

2x - 4 = 8

To solve a polynomial equation of the first degree, we must leave the unknown in the first member isolated. For this, we will take the number –4 from the first member, adding 4 to both sides, since –4 + 4 = 0.

2x - 4 = 8

2x - 4+ 4 = 8+ 4

2x = 12

Note that performing this process is equivalent to simply passing the number 4 with the opposite sign. So, to isolate the unknown x, let's pass the number 2 to the second member, since it's multiplying x. (Remember: the inverse operation of multiplication is division). It would be the same as dividing both sides by 2.

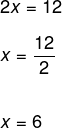
Therefore, the solution set is given by:

S = {6}

• Example 5

Solve equation 2^x+5 = 128 knowing that the universe set is given by U = ℝ.

To solve the exponential equation, let's first use the following potentiation property:

The^{m + n} = the^m · a^no

We will also use the fact that 2² = 4 and 2⁵ = 32.

2^x+5 = 128

2^x · 2⁵ = 128

2^x · 32 = 128

Note that it is possible to divide both sides by 32, that is, pass the number 32 to the second member by dividing.

So we have to:

2^x = 4

2^x = 2²

The only value of x that satisfies equality is the number 2, so x = 2 and the solution set is given by:

S = {2}

Equations are present in several fields of science.

solved exercises

question 1 – Consider the set universe U = ℕ and determine the solution of the following irrational equation:

Resolution

To solve this equation, we must be concerned with eliminating the root of the first member. Note that, for this, we need to raise the first member to the same index as the root, that is, to the cube. By the principle of equivalence, we must also raise the second member of equality.

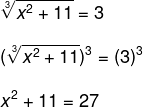
Note that we must now solve a polynomial equation of the second degree. Let's pass the number 11 to the second member (subtract 11 on both sides of the equality), in order to isolate the unknown x.

x² = 27 – 11

x² = 16

Now to determine the value of x, see that there are two values ​​that satisfy equality, x’ = 4 or x’’ = –4, once:

4² = 16

and

(–4)² = 16

However, note in the statement of the question that the given universe set is the set of natural numbers, and the number –4 does not belong to it, thus, the solution set is given by:

S = {4}

question 2 – Consider the polynomial equation x² + 1 = 0 knowing that the universe set is given by U = ℝ.

Resolution

For the equivalence principle, subtract 1 from both members.

x² + 1 – 1= 0 – 1

x² = – 1

Note that equality has no solution, since the universe set is the real numbers, that is, all the values ​​that the unknown can assume are real, and there is no real number that, when squared, is negative.

1² = 1

and

(–1)² = 1

Therefore, the equation has no solution in the set of reals, and thus we can say that the solution set is empty.

S = {}

by Robson Luiz
Maths teacher