THE rule of three is a method we use to find unknown values when we're working with quantities directly or inversely providesis. That resolution method has a lot of application not only in mathematics, but also in physics, chemistry and in everyday situations. Working with quantities is fundamental in several areas of knowledge, and, in the rule of three, it is important to be able to identify quantities that are directly related and quantities that are related in a way inverse.
Read too: Three Most Mistakes Made in the Rule of Three
Directly and inversely proportional quantities
THE comparison between two greatnesses is quite common and necessary in everyday life, and when we compare and check its proportion, we can separate them into two important cases: directly proportional quantities or inversely proportional.
- Directly proportional: as one of these quantities increases, the other also increases and in the same proportion. There are several situations in our daily life that involve directly proportional quantities, an example would be the price ratio and weight when buying a certain vegetable, the smaller the quantity, the lower the price, and the greater the quantity, the greater the price.
- Inversely proportional: as one of these quantities increases, the other quantity decreases accordingly. An example of this situation in everyday life is the relationship between speed and time. The greater the speed to travel a certain route, the shorter the time.
How to solve a simple rule of three?
To resolve situations using the rule of three, it is essential that there is proportionality, in addition, it is of great importance to identification of the relationship between the quantities.
Problems involving simple rule of three can be separated into two cases, when the quantities are directly proportional or inversely proportional. When faced with any issue that can be resolved with a rule of three, we follow these steps:
1st step – Identify the magnitudes and construction of the table.
2nd step – Analyze whether the quantities are directly or inversely proportional.
3rd step – Apply the correct solving method for each of the cases, and finally solve the equation.

Directly proportional quantities
Example:
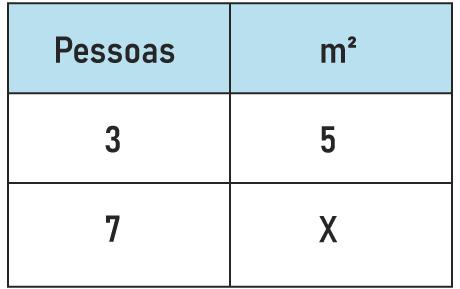
To revitalize a park, the community organized itself into a project known as Revitalize. In order for the project to be efficient, several fruit seedlings were collected. A plan for the planting was made, and in it 3 people worked in the planting and planted, per day, 5 m². Due to the need for more efficient planting, another 4 people, all with the same performance, pledged to participate in the cause, so what will be the amount of m² reforested per day?
The greats are people and reforested area.
Initially there were 3 people, and now there are 7.
Initially there were 5 m² of planting per day, but we do not know the amount of m² that will be cultivated by the 7 people, so we represent this value by x.
It is now essential to compare the two quantities. As I increase the number of people, the amount of m² reforested per day increases in the same proportion, so these quantities are directly proportional.

When the quantities are directly proportional, just multiply table values crosswise, generating the equation:
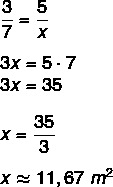
See too: What is proportion?
Inversely proportional quantities
Example:
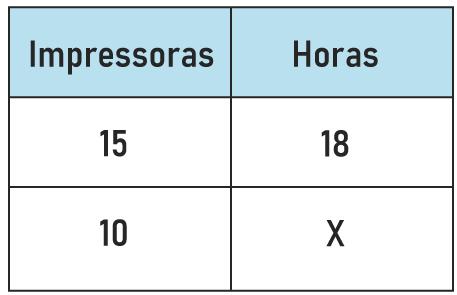
To prepare the tests for a competition, a printing company had 15 printers, which would take 18 hours to print all the tests. In preparation for the start of work, it was diagnosed that there were only 10 printers working. What is the time, in hours, that will be taken to prepare all the competition tests?
Quantities are quantities of printers and time.
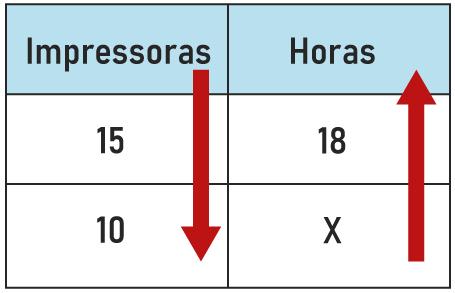
Analyzing the two magnitudes, it is clear that if the number of printers is reduced, consequently, the time to make prints will be increased, so these quantities are inversely proportional.
When the quantities are inversely proportional, it is necessary to invert the fraction (exchange numerator and denominator) of one of the fractions, to, later, multiply crossed.
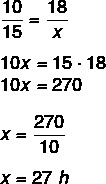
Tip: In summary, when the quantities are inversely proportional, we always invert one of the fractions and multiply crossed — detail forgotten for many problem solving and that makes many students make mistakes when they forget to analyze what kind of proportionality (direct or inverse) the problem is Working.
Simple and compound rule of three
There are two ways to apply the rule of three, the simple rule of three, when the problem involves two quantities, and the compound rule of three, when the problem involves more quantities. Then The rule of three compound is nothing more than an extension of the simple three rule when there is a greater number of magnitudes, and, to understand it, the simple rule of three is fundamental.
Also access: Percentage calculation with rule of three
solved exercises
Question 1 - On a farm with 800 chickens, 984 kg lasts exactly 10 days. If the farm had 200 more chickens, this ration would last:
A) 9 days
B) 8 days
C) 7 days
D) 6 days
E) 12 days
Resolution
Alternative B
First let's identify the quantities, they are: time and number of chickens. It is now possible to assemble the table and analyze whether they are directly or inversely proportional. We know that the greater the quantity of chickens, the less time the ration will last, so the quantities are inversely proportional.
The information on the amount of feed becomes irrelevant to answer the problem.
We know that 800 + 200 = 1000, and we want to find out how long the ration would last if they had 1000 chickens.
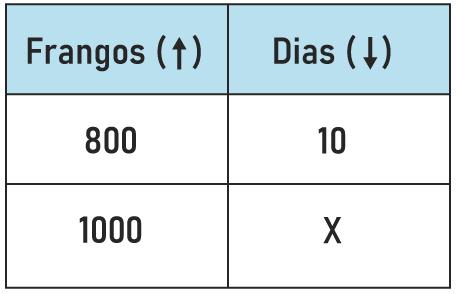
As they are inversely proportional, we will multiply straight:
1000x = 800 · 10
1000x = 8000
x = 8000: 1000
x = 8 days
Question 2 - To analyze the processes of traffic fines, the city had 18 employees, who were able to carry out the work on a daily basis, analyzing 135 processes. In one day, unfortunately, 4 employees did not attend. Assuming that all employees meet the same process demand, on that day, the number of processes analyzed will be:
A) 135
B) 120
C) 110
D) 105
E) 100
Resolution
Alternative D
Analyzing the situation, the quantities are: number of employees and number of processes. We know that the more employees we have, the more processes will be analyzed, so the quantities are directly proportional. 18 – 4 = 14 employees. Assembling the table, we have to:

As the quantities are directly proportional, we will multiply cross:
18x = 135 · 14
18x = 1890
x = 1890: 18
x = 105
By Raul Rodrigues de Oliveira
Maths teacher
Source: Brazil School - https://brasilescola.uol.com.br/matematica/regra-tres-simples.htm

