O fundamental principle of counting is the main concept taught in combinatorial analysis. It is from this that the other concepts in this area were developed and the factorial, combination, arrangement formulas, permutation. Understanding this principle is essential to understanding situations involving counting.
This principle states that if I need to make more than one decision and each one of them can be made in x, y, z ways, to to know how many ways these decisions can be taken simultaneously, just calculate the product of these possibilities.
Read too: Combinatorial analysis — what is it, important concepts, exercises

What is the fundamental principle of counting?
The fundamental principle of counting is a technique for calculating how many ways decisions can be combined. Whether a decision can be made from no ways and another decision can be made of m ways, the number of ways these decisions can be made simultaneously is calculated by the product of n · m.
Analyzing all possible combinations without using the fundamental principle of counting can be quite laborious, which makes the formula very efficient.
Example
In a restaurant, the famous dish is offered. All dishes have rice, and the customer can choose a combination of 3 meat options (beef, chicken and vegetarian), 2 types of beans (broth or tropeiro) and 2 types of drink (juice or soda). How many different ways can a customer place an order?
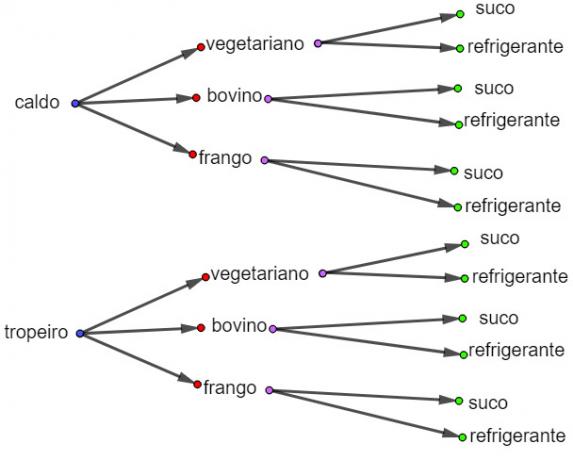
Note that there are 12 choices, but it was possible to reach this number by performing the simple multiplication of the possibilities through the fundamental principle of counting, so the number of possible combinations of dishes could be calculated by:
2 · 3 · 2 = 12.
Note that when my interest is to know only the total possibilities, multiplying is much faster than building any schema to analyze, which can be quite laborious if there are more and more possibilities.
When to use the fundamental principle of counting?
There are several applications of the fundamental principle of counting. It can be applied, for example, in various decisions of the Computing. An example are the passwords that require the use of at least one symbol, which makes the number of possible combinations much larger, making the system more secure.
Another application is in the study of odds.To calculate them, we need to know the number of possible cases and the number of favorable cases. The counting of this number of possible and favorable cases can be done through the fundamental principle of counting. This principle also generates the permutation formulas, combination and arrangement.
See too: Additive counting principle — union of one or more sets
solved exercises
1) (Enem) A school principal invited the 280 third-year students to participate in a game. Suppose there are 5 objects and 6 characters in a 9-room house; one of the characters hides one of the objects in one of the rooms of the house. The objective of the game is to guess which object was hidden by which character and in which room of the house the object was hidden.
All students decided to participate. Each time a student is drawn and gives his/her answer. The answers must always be different from the previous ones, and the same student cannot be drawn more than once. If the student's answer is correct, he is declared the winner and the game is over. The principal knows that some student will get the answer right because there is:
a) 10 students more than possible different answers.
b) 20 students more than possible different answers.
c) 119 students more than possible different answers.
d) 260 students more than possible different answers.
e) 270 students more than possible different answers.
Resolution
By the fundamental principle of counting, the number of possible answers will be equal to the product of the quantities of characters, objects and rooms.
5 · 6 · 9 = 270.
As the number of students is 280, then the difference between the number of students and the number of possibilities is 10.
Answer: alternative A.
2) (Enem) It is estimated that there are, in Acre, 209 species of mammals, distributed according to the table below.

We want to carry out a comparative study between three species of mammals – one from the Cetacean group, another from the Primate group and the third from the Rodent group. The number of distinct sets that can be formed with these species for this study is equal to:
a) 1320
b) 2090
c) 5840
d) 6600
e) 7245.
Resolution:
We know that there are 2 cetaceans, 20 primates and 33 rodents. So, by the fundamental principle of counting, the number of possible distinct sets will be:
2 ·20 ·33 = 1320
Answer: alternative A.
By Raul Rodrigues de Oliveira
Maths teacher
Source: Brazil School - https://brasilescola.uol.com.br/matematica/fatorial-principio-fundamental-da-contagem.htm

