Let's determine the area of a triangle from the point of view of analytic geometry. So, consider any three points, not collinear, A(xTheyThe), B(xByB) and C (xçyç). As these points are not collinear, that is, they are not on the same line, they determine a triangle. The area of this triangle will be given by:
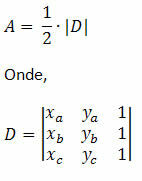
Note that the area will be half the magnitude of the determinant of the coordinates of points A, B, and C.
Example 1. Calculate the area of the triangle from vertices A (4, 0), B (0, 0) and C (0, 6).
Solution: First step is to calculate the determinant of the coordinates of points A, B and C. We will have:
Thus, we obtain:
Therefore, the area of the triangle of vertices A (4, 0), B (0, 0) and C (0, 6) is 12.
Example 2. Determine the area of the triangle of vertices A (1, 3), B (2, 5) and C (-2.4).
Solution: First, we must calculate the determinant.
Example 3. Points A (0, 0), B (0, -8) and C (x, 0) determine a triangle with an area equal to 20. Find the value of x.
Solution: We know that the area of the triangle of vertices A, B and C is 20. Then,
By Marcelo Rigonatto
Specialist in Statistics and Mathematical Modeling
Brazil School Team
Analytical Geometry - Math - Brazil School
Source: Brazil School - https://brasilescola.uol.com.br/matematica/area-um-triangulo.htm
