Polyhedra (from latin poly — many — and hedron — face) are figuresthree-dimensional formed by the union of regular polygons, in which the polyhedral angles are all congruent. The union of these polygons forms elements that make up the polyhedron, they are: vertices, edges and faces. However, not every three-dimensional figure is a polyhedron, an example of this are figures that have curved faces called round bodies.
There is a mathematical formula that relates the elements of a polyhedron called Euler's relationship. In addition, polyhedra are divided into two groups: the so-called polyhedra convex and the not convex. Some polyhedra deserve special attention, they are called Plato's polyhedra: tetrahedron, hexahedron, octahedron, dodecahedron and icosahedron.
Read too: Differences between flat and spatial figures
convex polyhedra
A polyhedron will be convex when formed by polygons convex, so that the following conditions are accepted:
- two of the polygons Never they are coplanar, that is, they do not belong to the same plane.
- Each side of one of these polygons belongs to only two polygons.
- The plane that contains any one of these polygons leaves the other polygons in the same half-space.

Read too:Sum of internal and external angles of a convex polygon
Elements of a convex polyhedron
Consider this convex polyhedron:

You quadrilaterals in the figure are called faces of the polyhedron.
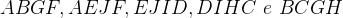
You pentagons are the faces and the base of the polyhedron, which is named pentagonal base polyhedron.
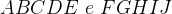
The segments that form each of the faces are called edges of the polyhedron.
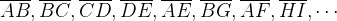
The points where the edges meet are called vertices.
The line segment JC will be called diagonal of the polyhedron, denoted by:

JC is one of the diagonals, we understand diagonal of the polyhedron as being the line segment that joins two vertices not belonging to the same face.
We also have the polyhedral angle, formed between the edges, denoted by:

A polyhedral angle is called a trihedral When three edges originate from a vertex. Likewise, it is called tetrahedral, case four edges originate from a vertex, and so on.
From now on, we will establish some notations, they are:
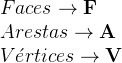
Know more: Planning of geometric solids
Properties of a Convex Polyhedron
Property 1
The sum of the edges of all faces is equal to twice the number of edges of the polyhedron.
Example
A polyhedron has 6 square faces. Let's determine the number of edges.
According to the property, just multiply the number of edges of a face by the number of faces, and this is equal to twice the number of edges. Thus:

Property 2
The sum of the vertices of all faces is equal to the sum of the edges of all faces, which is equal to twice the number of edges.
Example
A polyhedron with 5 tetrahedral angles and 4 hexahedral angles. Let's determine the number of edges.
Analogous to the previous example, the second property says that the sum of the edges of all the faces is equal to twice the number of edges. The number of edges is given by the product of 5 by 4 and 4 by 6, as they are 5 tetrahedral and 4 hexahedral angles. Thus:
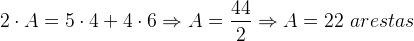
Concave (non-convex) polyhedra
A polyhedron is non-convex, or concave, when we take two points on distinct faces and the straight r that contains these points is not all contained in the polyhedron.

Note that the straight line (in blue) is not complete in the polyhedron, so the polyhedron (in pink) is concave or non-convex.
regular polyhedra
We say that a polyhedron is regular when your faces are regular polygons equal to each other and with the polyhedral angles all the same.
See some examples:
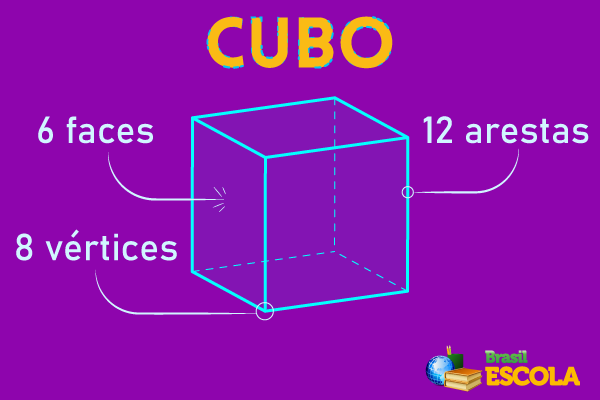
Notice that all your faces are regular polygons. Its faces are formed by squares and the edges are all congruent, that is, they have the same measure.
readalso: What are regular and convex polygons?
Euler's relationship
Also known as Euler's theorem, the result was proved by Leonhard Euler (1707 - 1783) and guarantees that in all closed convex polyhedron the following relationship is valid:
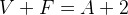
Plato's Polyhedra

Any polyhedron that satisfies the following conditions is called Plato's polyhedron:
The Euler relation is valid
All faces have the same number of edges
All polyhedral angles have the same number of edges
It is proven that there are only five regular and convex polyhedra, or Plato's polyhedra, they are:
regular tetrahedron

the tetrahedron has 4 triangular faces congruent and 4 trihedral angles congruent.
regular hexahedron

the hexahedron has 6 square faces congruent and 8 trihedral angles congruent.
regular octahedron

the octahedron has 8 triangular faces congruent and 6 tetrahedral angles congruent.
regular dodecahedron

the dodecahedron has 12 pentagonal faces congruent and 20 anglestrihedral congruent.
regular icosahedron

The icosahedron has 20 triangular faces congruent and 12 pentahedral angles congruent.
solved exercises
1) (Enem) A jewel was cut in the form of a 32-face convex polyhedron, 20 of which are hexahedra and the rest are pentagonal. This jewel will be a gift for a lady who is celebrating her birthday, completing an age whose number is the number of vertices of this polyhedron. This lady is completing:
a) 90 years
b) 72 years old
c) 60 years old
d) 56 years old
e) 52 years old
Solution:
Gives property 1 of convex polyhedra we know that:
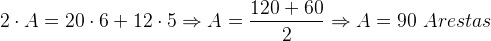
Now how we know the number of edges it's the number of faces, we can use the Euler relation.

As the age you are completing is equal to the number of vertices, so this is 60 years. Alternative c.
2) (PUC-SP) How many edges does a convex polyhedron with triangular faces where the number of vertices is three-fifths the number of faces?
a) 60
b) 30
c) 25
d) 20
e) 15
Solution:
From the properties of a convex polyhedron and the exercise statement we have:

Substituting these values in the Euler relation, we have the following:
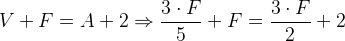
Organizing the previous equation and solving the equation in F, it follows that:

Substituting the value of the number of faces found in the equation of edges, we will have:
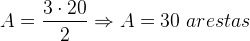
Alternative b
by Robson Luiz
Maths teacher

