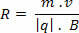O center of mass of a body is a point that behaves as if the entire mass of the body were concentrated on it. When an object is homogeneous, the center of mass coincides with its geometric center. However, this is not always the case, and the center of mass does not even need to be inside the body.
Now that we know that the center of mass depends on the distribution of pasta of a body, let's see the different ways to perform its calculation in a system.
Center of mass of a set of particles
Let's initially analyze the center of mass of a system of particles in the same plane, as shown in the following figure:

Diagram for calculating the center of mass in a set of particles
Point C, located at an intermediate point in the set of particles, represents the center of mass of this system. The coordinates of this point (xCMyCM) are calculated from the weighted averages, according to the following equations:
xCM = m1x1 + m2x2 + m3x3
m1 + m2 + m3
yCM = m1y1 + m2y2 + m3y3
m1 + m2 + m3
This equation can be used for any number of particles.
Center of mass of flat figures
Another case to be analyzed is the calculation of the center of mass of plane figures. In general, we use the following rule:
“ The center of mass of a flat homogeneous figure is located on its axis of symmetry¹. If the body has two symmetry axes, the center of mass will be at the intersection between the axes.”
¹Symmetry axis is a line that divides a body into two equal or symmetrical parts.
Note in the figures below where the symmetry axes and their respective centers of mass are located:
Rectangle
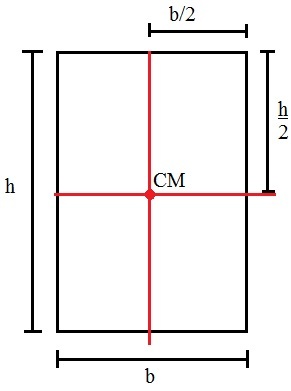
Diagram representing the center of mass of the rectangle
The rectangle's center of mass lies on the symmetry axes that halve height (h) and base (b). So, to calculate it, just divide the height and the base by two.
Circle
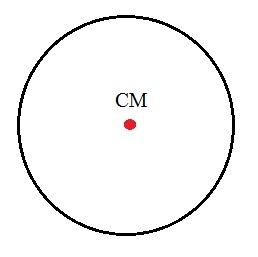
Diagram representing the center of mass of the circle
Do not stop now... There's more after the advertising ;)
The center of mass of the circle is exactly at its center because the circle axis of symmetry it is a straight line that goes from one of its ends to the other, passing exactly through its center.
triangle

Diagram representing the center of mass of a right triangle
Since the base of the right triangle is wider, most of its mass is at the bottom. As shown in the figure, the right triangle's center of mass is located one-third of its height and base.
Center of mass of composite plane figures
To calculate the center of mass of composite plane figures, we must consider each part of the figure individually, find its centers of mass and then add them up. For this, we must adopt a reference system, as shown in the figure:
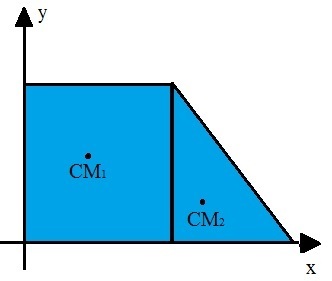
Diagram of the center of mass of a composite figure
The image above shows a flat figure made up of a square and a right triangle. After adopting the frame of reference (x, y), we must consider the center of mass of each of the figures. For this, we use the index 1 for the square and 2 for the triangle. To calculate the coordinates of the center of mass of the entire figure, we must add the coordinates of the individual figures through the equation:
xCM = m1x1 + m2x2
m1 + m2
yCM = m1y1 + m2y2
m1 + m2
We can see the existence of the center of mass when observing a children's toy called joão-bobo, which is a plastic or wooden doll with a rounded base. Even if he is pushed, swayed or tilted, the “joão-bobo” returns and stands up. This is because most of your weight is located at your base, which makes your center of mass close to the ground, that is, close to your support point.
Knowing the center of mass is important even for our own health: the center of mass of the human body is at the height of the spine, so when lifting objects heavy, bending the knees is recommended, which causes a redistribution of our mass due to the change in the center of mass of our body, thus not causing damage to the column.
By Mariane Mendes
Graduated in Physics
Would you like to reference this text in a school or academic work? Look:
TEIXEIRA, Mariane Mendes. "Center of mass"; Brazil School. Available in: https://brasilescola.uol.com.br/fisica/centro-massa.htm. Accessed on June 27, 2021.