O triangle it is a polygon formed by three sides. This means that it is a flat geometric figure formed by three straight segments which meet at their ends, also forming three vertices and three internal angles. THE area of a triangle is the amount of flat that polygon occupies in the space where it is defined.
Thus, the area is a number that is related to the amount of flat occupied by the geometric figure. The larger the area of the figure, the greater the space it occupies and vice versa.
Fundamentals for calculating the area
The first step in determining the area of any geometrical figure is to establish a unit of measurement of length, which will be used to define the area measurement unit.
After that, build a square that has the side measurement equal to 1 unit of the established measurement unit. For example, setting the unit of measure as centimeter, this square should be 1 centimeter on a side.
That square will be the base unit of measure for the area of any geometry. This area measurement unit is now called
centimetersquare (cm2). Therefore, measuring the area of a figure in square centimeters is the same as determining the number of squares on the side. equal to 1 cm that "fits" inside this figure, with no spaces between the squares or that they remain superimposed.In practice, it is not necessary to think about it every time you need to calculate the area of some figure. In some of them - especially in triangles – it is not even possible to fill with squares without any part of the square being left out of the figure, or in such a way that the entire figure is occupied by squares of side 1 un, as shown in figure a follow.
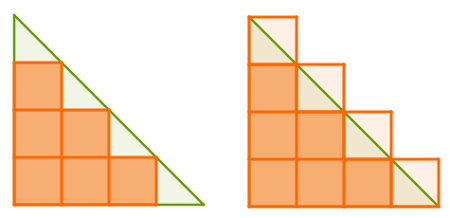
In the two cases shown above, using the technique mentioned, it cannot be said that the area of triangle green is 9 and it can't be said to be 16 either. To eliminate this problem, there is a formula to calculate the triangle area.
Do not stop now... There's more after the advertising ;)
triangle area
The formula that can be used to calculate the area of the triangle is as follows:
A = bh
2
In this formula, b is the measure of the base of the triangle and h is the measure of its height. This formula is obtained through three steps:
The first is to determine the areaofrectangle. Note that counting the number of squares used to fill a rectangle is the same as multiplying its length by its width, or in other words, its base by its height.
The second is to use the areaofrectangle and the decomposition of geometric figures to determine the areaofparallelogram, which is also the product of its base for its height.
The third is just realizing that every triangle is equal to half of one parallelogram, cut by one of its diagonals.
Examples:
1- Determine the area of a triangle whose base measures 10 cm and the height also measures 10 cm.
Solution:
A = bh
2
A = 10·10
2
A = 100
2
H = 50 cm2
2- What is the area of a triangle that has two sides measuring 5 m and one side measuring 6 m?
Solution:
That triangle is isosceles. Assuming your base is the side that measures 6 meters, we will build the height relative to that base. Exactly because the triangle is isosceles, we can guarantee that this height is also the median of the base by dividing it in two. segments that measure 3 meters.
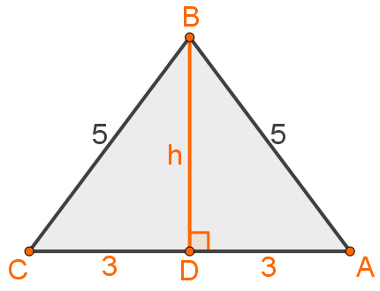
Thus, this construction forms the triangle ABD. Applying the Pythagorean theorem, we have:
52 = h2 + 32
25 = h2 + 9
25 - 9 = h2
16 = h2
h = 4 m
knowing the height and the base of triangle, we can calculate your area:
A = bh
2
A = 6·4
2
A = 24
2
H = 12 m2
By Luiz Paulo Moreira
Graduated in Mathematics
Would you like to reference this text in a school or academic work? Look:
SILVA, Luiz Paulo Moreira. "What is the area of the triangle?"; Brazil School. Available in: https://brasilescola.uol.com.br/o-que-e/matematica/o-que-e-area-triangulo.htm. Accessed on June 27, 2021.

