the understanding of sets is the main basis for the study of algebra and concepts of great importance in Mathematics, such as functions and inequalities. The notation we use for sets is always an uppercase letter from our alphabet (eg set A or set B).
In terms of representation of sets, it can be done by venn diagram, by simply describing the characteristics of its elements, by enumerating the elements or by describing their properties. When working with problems that involve sets, there are situations that require the performance of operations between sets, being the union, the intersection and the difference. Are we going to study all this in detail?
See too: Numeric expressions – learn to solve them!
Notation and representation of sets
For representation of a set, we always use a capital letter of the alphabet, and the elements are always between keys and are separated by a comma. To represent the set of even numbers greater than 1 and less than 20, for example, we use the following notation: P ={2,4,6,8,10,12,14,16,18}.
Forms of representation of sets
representation by enumeration: we can enumerate its elements, that is, make a list, always between braces. See an example:
A = {1,5,9,12,14,20}
describing the features: we can simply describe the characteristic of the set. For example, let X be a set, we have that X = {x is a positive number multiple of 5}; Y: is the set of months of the year.
Venn Diagram: sets can also be represented in the form of a diagram, known as a venn diagram, which is a more efficient representation for performing operations.
Example:
Given the set A = {1,2,3,4,5}, we can represent it in the following Venn diagram:
Elements of a set and membership relationship
Given any element, we can say that the element belongs to the set or not belong to that set. To represent this membership relationship more quickly, we use the symbols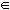
(read as belonging) and ∉ (read as not belonging). For example, let P be the set of pair numbers, we can say that the 7 ∉ P and that 12 P.
Equality of sets
Comparison between sets is inevitable, so we can say that two sets are equal or not, checking each of its elements. Let A = { 0,1,3,4,8} and B = { 8,4,3,1,0}, even if the elements are in different order, we can say that the sets A and B are equal: A = B.
Inclusion relationship
When comparing two sets, we can come across several relationships, and one of them is the inclusion relationship. For this relationship, we need to know some symbols:
⊃ → contains ⊂→ is contained
⊅ → does not contain ⊄→is not contained
Tip: The opening side of the symbol will always face the larger set. |
When all the elements of a set A also belong to a set B, we say that A ⊂ B or that A is contained in B. For example, A={1,2,3} and B={1,2,3,4,5,6}. It is also possible to perform the representation by venn diagram, that would look like this:
A is contained in B:
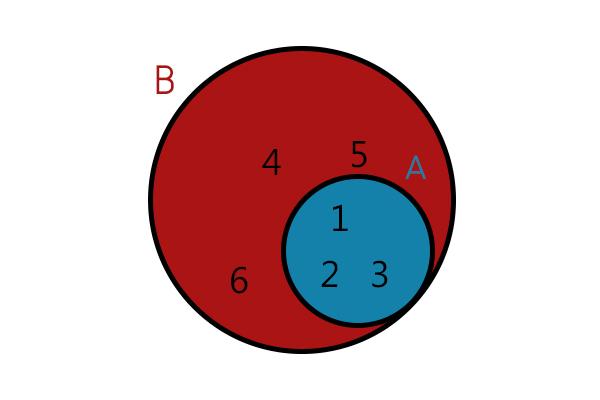
A ⊂ B
Subsets
When a inclusion relationship, that is, the set A is contained in the set B, we can say that A is a subset of B. The subset remains a set, and a set can have multiple subsets, built from the elements belonging to it.
For example: A: {1,2,3,4,5,6,7,8} has as subsets the sets B: {1,2,3}; C: {1,3,5,7}; D: {1} and even the set A {1,2,3,4,5,6,7,8}, that is, A is a subset of itself.
unitary set
As the name already suggests, it's that set that has only one element, like the set D:{1} shown earlier. Given the set B: {1,2,3}, we have the subsets {1}, {2} and {3}, which are all unit sets.
ATTENTION: The set E: {0} is also a unitary set, as it has a single element, “0”, and it is not an empty set.
Read too: Set of integers - elements and characteristics
empty set
With an even more suggestive name, the empty set has no elements and is a subset of any set. To represent the empty set, there are two possible representations, they are V: { } or the symbol Ø.
Part sets
We know as sets of parts all possible subsets of a given set. Let A: {1,2,3,4}, we can list all subsets of this set A starting with the sets that have no elements (empty) and then those that have one, two, three and four elements, respectively.
empty set: { };
Unit sets: {1}; {2};{3}; {4}.
Sets with two elements: {1,2}; {1,3}; {1,4}; {2,3}; {2,4}; {3,4}.
sets with three elements: {1,2,3}; {1,3,4}; {1,2,4}; {2,3,4}.
Set with four elements: {1,2,3,4}.
Therefore, we can describe the set of parts of A in this way:
P: { { }, {1}, {2}, {3}, {4}, {1,2}, {1,3}, {1,4}, {2,3}, {2,4 }, {3,4}, {1,2,3}, {1,3,4}, {1,2,4}, {2,3,4}, {1,2,3,4} }
To find out how many parts it is possible to divide a set, we use the formula:
n[P(A)] = 2no
The number of parts of A is calculated by a potency base 2 raised to no, on what no is the number of elements in the set.
Consider the set A: {1,2,3,4}, which has four elements. The total of possible subsets of this set is 24 =16.
Read too: What is the set of irrational numbers?
Finite and Infinite Set
When working with sets, we find sets that are limited (finite) and those who are unlimited (infinite). The set of even or odd numbers, for example, is infinite and, to represent it, we describe some of its elements in sequence, so that it is possible to predict what the next elements will be, and we put ellipses in the Final.
I: {1,3,5,7,9,11...}
P: {2,4,6,8,10, ...}
In a finite set, however, we do not put the ellipses at the end, as it has a defined beginning and end.
A: {1,2,3,4}.
universe set
O universe set, denoted by U, is defined as the set formed by all the elements that must be considered within a problem. Every element belongs to the universe set and every set is contained in the universe set.
Operations with sets
The operations with sets are: union, intersection and difference.
Intersection of sets
An intersection occurs when elements belong simultaneously to one or more sets. When writing A∩B, we are looking for elements that belong to both set A and set B.
Example:
Consider A= {1,2,3,4,5,6} and B = {2,4,6,7,8}, the elements that belong to both set A and set B are: A∩B = { 2,4,6}. The representation of this operation is done as follows:
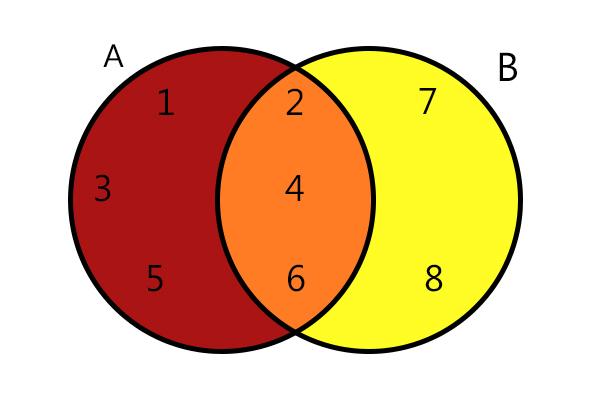
A∩B
When sets do not have any elements in common, they are known as disjoint sets.
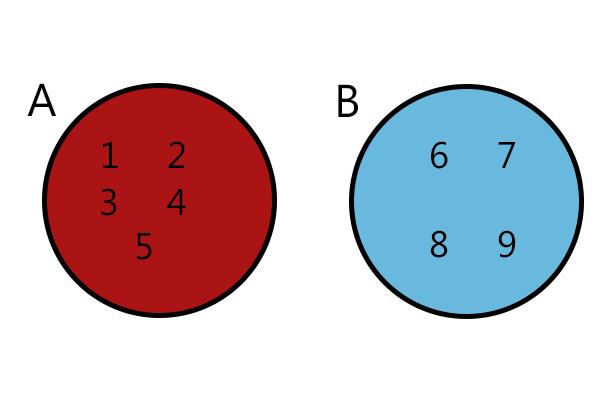
A∩B = Ø
difference between sets
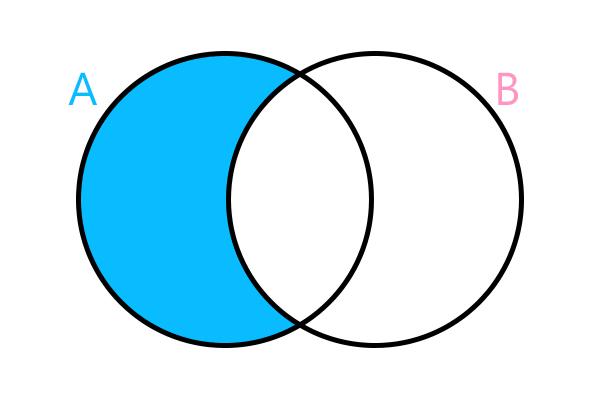
calculate the difference between two sets is to look for elements that belong to only one of the two sets. For example, A – B has as an answer a set composed of elements that belong to set A and do not belong to set B.
Example: A: {1,2,3,4,5,6} and B: {2,4,6,7,8}. Note that A ∩ B ={2,4,6}, so we have that:
a) A - B = { 1,3,5 }
b) B – A = {7,8}
Unity
The union of two or more sets is the joining your terms. If there are elements that are repeated in both sets, they are written only once. For example: A={1,2,3,4,5} and B={4,5,6,7,10,14}. To represent the union, we use the symbol (reads: A union with B).
A U B = {1,2,3,4,5,6,7,10,14}
To learn more about these operations and check out several solved exercises, read: Operations with sets.
Morgan's Laws
Let A and B be two sets and let U be the universe set, there are two properties that are given by Morgan's Laws, namely:
(A U B)ç = Aç ∩Bç
(A ∩ B)ç = Aç U Bç
Example:
Given the sets:
U: {1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20}
A: {2,4,6,8,10,12,14,16,18,20}
B: {5.10,15,20}
Let's check that (A U B)ç = Aç ∩Bç. So, we have to:
A U B = {2,4,5,6,8,10,12,14,15,16,18,20}
Therefore, (A U B)ç={1,3,7,9,11,13,17,19}
To check the veracity of equality, let's analyze operation Aç ∩Bç:
THEç:{1,3,5,7,9,11,13,15,17,19}
Bç:{1,2,3,4,6,7,8,9,11,12,13,14,16,17,18,19}
Then, THEç ∩Bç ={1,3,7,9,11,13,15,17,19}.
(A U B)ç = Aç ∩Bç
solved exercises
01) Consider U: {1,2,3,4,5,6,7,8,9,10}, A: {1,2,3,4,5,6} and B: {4,5,6, 7,8,9}. Show that (A ∩ B)ç = Aç U Bç.
Resolution:
1st step: find (A ∩ B)ç. For that, we have that A ∩ B = {4,5,6}, so (A ∩ B)ç ={1,2,3,7,8,9,10}.
2nd step: find Aç U Bç. THEç:{7,8,9,10} and Bç:{1,2,3,10}, so Aç U Bç = {1,2,3,7,8,9,19}.
It is shown that (A ∩ B)ç = Aç U Bç.
02) Knowing that A is the set of even numbers from 1 to 20, what is the total number of subsets we can build from the elements of that set?
Resolution:
Let P be the set described, we have that P: {2,4,6,8,10,12,14,16,18,20}. Therefore, the number of elements of P is 10.
By the set of parts theory, the number of possible subsets of P is:
210=1024
By Raul Rodrigues de Oliveira
Maths teacher