We have that a complete turn on the trigonometric circle corresponds to 360º or 2π rad, according to the following illustration:
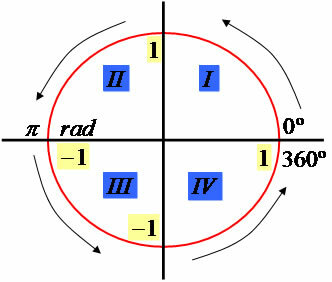
Note that the circle has a radius measuring one unit and is divided into four quadrants, facilitating the location of trigonometric angles, according to the following situation:
1st quadrant: positive abscissa and positive ordinate → 0º < α < 90º.
2nd quadrant: negative abscissa and positive ordinate → 90º < α < 180º.
3rd quadrant: negative abscissa and negative ordinate → 180º < α < 270º.
4th quadrant: positive abscissa and negative ordinate → 270º < α < 360º.
In trigonometric studies there are arcs that have measures greater than 360º, that is, they have more than one turn. We know that a complete lap is equivalent to 360º or 2π rad, based on this information we can reduce it to the first lap, performing the following calculation: divide the arc measure in degrees by 360º (full turn), the remainder of the division will be the smallest positive determination of the arc. In this way, the main determination of the arc in one of the quadrants is easier.
Example 1
Determine the main location of the 4380° arc using the rule of thumb.
4380º: 360º corresponds to 4320º + 60º, so the remainder of the division is equal to 60º which is the main determination of the arc, thus, its extremity belongs to the 1st quadrant.
Example 2
What is the main determination of the arc with a measure equal to 1190º?
1190º: 360º, the division has a result equal to 3 and the remainder 110, we conclude that the arc has three complete turns and an end at an angle of 110º, belonging to the 2nd quadrant.
congruent arches
Two arcs are congruent when they have the same origin and the same end. An effective rule of thumb for determining whether two arcs are congruent is to check whether the difference between them is a divisible number or multiple of 360º, that is, the difference between the measurements of the arcs divided by 360º must have a remainder equal to zero.
Example 3
Check that the arcs measuring 6230º and 8390º are congruent.
8390º – 6230º = 2160
2160º / 360º = 6 and remainder equal to zero. Therefore, the arcs measuring 6230º and 8390º are congruent.
Example 4
Check that the 2010º and 900º arcs are congruent.
2010º – 900º = 1110º
1110º / 360º = 3 and remainder equal to 30. Therefore, the arcs are not congruent.
by Mark Noah
Graduated in Mathematics
Brazil School Team
Trigonometry - Math - Brazil School
Source: Brazil School - https://brasilescola.uol.com.br/matematica/arcos-mais-de-uma-volta.htm

