When it is necessary to relate a side to a angle on one right triangle in order to find the measurements of one of its sides or one of its angles, we can use the trigonometric relations: sine, cosine and tangent. It is also possible to calculate the measure of one of the sides or one of the angles of a triangleany, that is, not necessarily of a right triangle. For this, one of the methods used is the sins law.
sins law
Take the triangle ABC as an example, registered in a circumference of radius r.

In a case like this, the sides and angles have any measures. So we have:
The = B = ç = 2r
sinα sinβ sinθ
In this triangle, a, b, and c are the measurements of its sides; α, β and θ are their internal angles, and the sines of these angles have the same values as the sines found in the tablestrigonometric.
at first fraction, a is the measure on the opposite side of sinα; in the second fraction, b is the measure opposite sinβ, and in the third fraction, note that c is the measure opposite sinθ. So there is a
proportion between the ratios formed by the measure of one side and the sine of the angle opposite to that measure.Also note that each of these ratios is equal to the diameter of the circle circumscribing the triangle.
Most of the time it is necessary to calculate the measure of one side of a triangle, knowing the measurements from an angle opposite to it, from the other side and from the angle opposite to that other side, we should use The sins law. This law can also be used to find the measure of one of the angles of a triangle, if we know the measurements from another angle and from the opposite sides of these two angles.
Examples
1 – Calculate the measure of side AB on the triangle Next.

Note that side AB, represented by x, is opposite to angle 45°, and the CB side, which measures 10 cm, is opposite the 30° angle. So we can use the lawFromsines:
The = B
sinα sinβ
x = 10
sen45 sen30
Using the fundamental property of proportions, we have:
x·sen30 = 10·sen45
In the table of values trigonometric notable, sen45 = √2/2 and sen30 = 1/2. Replacing these values, we have:
x = 10√222
x = 10√2 cm
2 – Calculate the CB side measurement on the triangle Next.
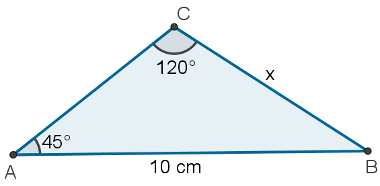
Side CB, represented by x, is opposite the 45° angle. Also note that side AB, which measures 10 cm, is opposite the 120° angle. Using the lawFromsines, we can write:
The = B
sinα sinβ
x = 10
sen45 sen120
x·sen120 = 10·sen45
To continue, remember that senx = sin (180 – x), therefore: sin120 = sin (180 – 120) = sen60. Replacing the value, we have:
x·sen60 = 10·sen45
x·√3 = 10·√222
x·√3 = 10·√2
x = 10·√2
√3
x = 10√3√2
3
x = 10√6
3
By Luiz Paulo Moreira
Graduated in Mathematics
Source: Brazil School - https://brasilescola.uol.com.br/o-que-e/matematica/o-que-lei-dos-senos.htm
