The definition of limit is used in order to expose the behavior of a function at times of approximation of certain values. The limit of a function is of great importance in differential calculus and in other branches of mathematical analysis, defining derivatives and continuity of functions.
We say that a function f(x) has a limit A when x → a (→: tends), that is,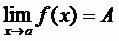
, if, tending x to its limit, in any case, without reaching the value a, the magnitude of f(x) – A becomes and remains smaller than any predetermined positive value, however small.
theorems
1 – The sum limit of two or more functions of the same variable must be equal to the sum of their limits.
2 – The limit of the product of two or more functions of the same variable must be equal to the multiplication of their limits.
3 – The limit of the quotient of two or more functions of the same variable must be equal to the division of their limits, emphasizing that the limit of the divisor is different from zero.
4 – The positive root limit of a function is equal to the same root as the function limit, remembering that this root must be real.
We must be careful not to assume that 
, because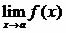 
depends on the behavior of f(x) for values of x close to but different from a, while f(a) is the value of the function at x = a.
Determining the limit of a function
by Mark Noah
Graduated in Mathematics
Brazil School Team
Roles - Math - Brazil School
Source: Brazil School - https://brasilescola.uol.com.br/matematica/limite-uma-funcao.htm
