escape velocity, also known as cosmic first velocity, is the minimum speed that some object without propulsion needs to be able to escape the gravitational attraction of massive bodies, such as planets and stars. the escape velocity is scalar greatness which can be calculated when all the kinetic energy of a body is converted into the form of gravitational potential energy.
See too: Five Physics Discoveries That Happened By Accident
How is the escape velocity calculated?
The escape velocity is obtained by assuming that the entire energykinetics present at the instant of release of a body is transformed into energypotentialgravitational, therefore, we disregard the action of forcesdissipative, like the drag donate.

Despite being a velocity, the escape velocity is climb, since she it doesn't depend on the direction to which the body is launched: be a vertical launch, or even in the direction tangential, how fast the body needs to be, so that it can escape the gravitational field, is the same.
In addition to not depending on the launching direction, the escape velocity also depends on the body mass, but on the pastaofplanet.
Below is the calculation that is done to determine the escape velocity formula, to do this, we equate the kinetic energy with the gravitational potential energy, observe:

M and M – body and planet mass, respectively (kg)
g – gravity acceleration (m/s²)
G – constant of universal gravitation (6.67.10-11 Nm²/kg²)
R – distance from the center of the planet (m)
v – escape velocity (m/s)
The calculation shown took into account the formula of gravity, given by the ratio between the planet's mass and the square of its average radius, multiplied by the constantgravitational. The result obtained shows that the escape velocity depends only on the lightning and of the pasta of the planet, so let's calculate what is the escape velocity of a body that is projected from the Earth's surface at sea level:
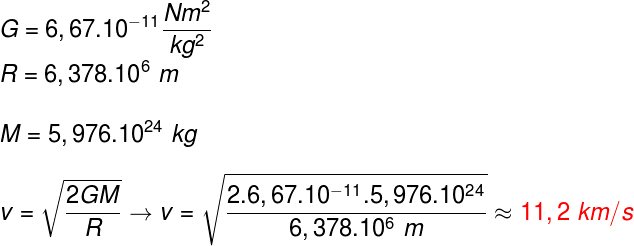
The presented calculation shows that if an object is launched from the Earth's surface, with a minimum velocity of 11.2 km/s, in the absence of dissipative forces, this body will escape from Earth's orbit.
See too: What are black holes and what do we know about them?
Orbital velocity or second cosmic velocity
Speedorbital, also known as velocitycosmicMonday, is the speed with which an orbiting object moves around its star. Orbital speed is always tangentàtrajectory of the body in orbit, to calculate it, we say that the gravitational pull force it's equivalent to centripetal force, which keeps the body in circular motion or on an elliptical trajectory, for example.
Below, we show the formula that is used to calculate the orbital velocity, note:

The formula takes into account the mass of the star in which a body orbits, as well as the radius of its orbit, measured from the center of that star. From this formula and the one used to calculate the velocityinexhaust, it is possible to establish a relationship between these two speeds, this relationship is shown below:

solved exercises
Question 1)(who) A book by the American science fiction writer Robert Anson Heinlein (1907-1988) reads: “The choice of staff for the first human expedition to Mars was made based on the theory that the greatest danger to man was man himself. men. At that time – eight Earth years after the founding of the first human colony on Luna – an interplanetary journey of human beings must have been made in free-fall orbits, taking, from Earth to Mars, one hundred and fifty-eight Earth days and vice versa, plus a wait on Mars from one hundred and fifty-five days, until the planets slowly returned to their previous positions, allowing the existence of a return orbit.” (adapted)
(HEINLEIN, R. THE. A stranger in a strange land. Rio de Janeiro: Artenova, 1973, p. 3).
Consider the ratio between the masses of Earth and Mars equal to 9 and the ratio between the rays of Earth and Mars equal to 2 consider, further, that there are no frictional forces and that the a body's escape velocity is the minimum velocity with which it must be launched from the surface of a star so that it can overcome the gravitational pull of this star.
Check what is correct.
01) The escape velocity of a body is directly proportional to the square root of the ratio between the planet's mass and radius.
02) The escape velocity of a spacecraft from the Earth's surface is lower than the escape velocity with which the same spacecraft must be launched from the surface of Mars.
04) The escape velocity of a spacecraft does not depend on its mass.
08) For a spacecraft to orbit the planet Mars, its speed must be proportional to the radius of the orbit.
16) A spacecraft with its engines turned off and approaching Mars is subject to a force that depends on its speed.
The sum of the correct alternatives is equal to:
a) 12
b) 3
c) 5
d) 19
e) 10
Solution
Alternative C.
Let's analyze each of the alternatives:
01 – REAL – The escape velocity formula depends on the square root of the planet's mass by its radius.
02 – FALSE – To verify this, it is necessary to use the escape velocity formula, taking into account that the Earth's mass is 9 times the mass of Mars and the radius of the Earth is 2 times the radius of Mars:
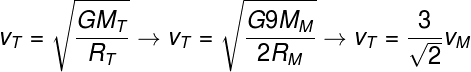
According to the resolution, Earth's escape velocity is greater than Mars' escape velocity, so the statement is false.
04 – REAL – We only need to analyze the escape velocity formula to see that it only depends on the planet's mass.
08 – FALSE – The orbital velocity must be inversely proportional to the square root of the orbital radius.
16 – FALSE – The force that attracts the spacecraft to Mars is gravitational and its magnitude can be calculated according to the Law of Universal Gravitation. According to this law, gravitational attraction is proportional to the product of masses and inversely proportional squared of the distances, nothing about the velocity magnitude is mentioned in this law, so the alternative is false.
The sum of the alternatives is equal to 5.
Question 2) (Cefet MG) A rocket is launched from a planet of mass M and radius R. The minimum speed needed for it to escape the gravitational pull and go into space is given by:
The)
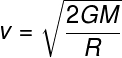
B)
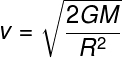
ç)
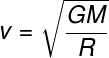
d)

and)

Solution
Alternative C.
The formula used to calculate the escape velocity is shown in the letter C, as explained in the article.
By Rafael Hellerbrock
Physics teacher
Source: Brazil School - https://brasilescola.uol.com.br/fisica/velocidade-escape.htm