THE equation in Torricelli is an equation of Kinematics developed by the Italian physicist and mathematician Evangelista Torricelli. This equation allows you to determine quantities such as acceleration, speedsFinal and initial and even the displacement of a body that moves with constant acceleration when you don't know the breakintime in which the movement took place.
Torricelli Equation Summary
THE equationinTorricelli it can be used in exercises that involve constant accelerations in cases where the time interval is not informed.
Using the equationinTorricelli, we can determine quantities such as initial velocity, final velocity, acceleration and displacement.
To determine the equationinTorricelli, we use the hourly function of position and the hourly function of velocity.
The graph of equationinTorricelli in velocityin function oftime is always a straightascendant or downward for the cases of movements accelerated and slowed down, respectively.
Torricelli Equation
Torricelli's equation is independent of time. It is developed from the joining of the clockwise function of velocity with the clockwise function of the position for the
movementevenlyvaried (MUV), that is, a movement that occurs in a straight line and with accelerationconstant. Torricelli's equation is defined by the formula below: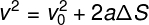
Subtitle:
v – final speed (m/s)
v0 – initial speed (m/s)
The – average acceleration (m/s²)
S – displacement (m)
Lookalso:How to solve Kinematics exercises?
Determination of the Torricelli Equation
To determine the equationinTorricelli, we use the MUV speed hourly function with the position hourly function. The process is simple: we isolated the variable t (time) in the hourly velocity function and we substitute this unknown in the hourly velocity function.
The equation below shows the hourly function of the velocity of the MUV:
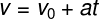
Subtitle:
v – final speed (m/s)
v0 – initial speed (m/s)
The – average acceleration (m/s²)
t – time interval(s)
Below, we have the occupationhourlygivesposition to MUV:

Subtitle:
s – final position (m)
s0 – starting position (m)
v0 – initial speed (m/s)
The – average acceleration (m/s²)
t – time interval(s)
We isolated the variable t at occupationhourlygivesvelocity:

Then we replace the variable t at occupationhourlygivesposition. In this way, we will have the following development:

By squared the second term in parentheses and applying the distributive property, we will have the following solution for the above equation:

By doing the substitutions correctly, we can determine a very useful, time-independent equation for the MUV. To do so, just know the functions of the velocity and of the position of the movement evenlymiscellaneous.
Lookalso:Seven “Golden” Tips for a More Effective Physics Study
Torricelli Equation Graphs
The most common Torricelli equation graphs are those that relate the rover's speed to time. Through these graphs, it is also possible to determine the Torricelli equation. Watch:

The graph above shows the speed of a body steadily increasing as a function of time. This indicates that its acceleration does not vary and that this movement is uniformly accelerated.
We can determine the space covered by the furniture represented in the graph through its area. Therefore, it is important to note that the figure shown above is shaped like a trapeze, whose area is determined by the following formula:
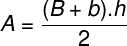
Subtitle:
THE – trapeze area
B – edge of the larger base of the trapeze
B – edge of the lower base of the trapeze
H – trapeze height
Looking calmly at the figure, we notice that this trapeze is lying down, its larger and smaller base edges are vf and v0, respectively, and its height is the time interval t. Thus, the area of this geometric figure is given by:

With the same device used to determine the equationinTorricelli previously, we replaced t:

In this way, we will have the following equation:

The solution of this equation, after applying the distributive properties, results in the Torricelli equation.
Lookalso: The most common mistakes when studying Physics
Torricelli Equation Exercises
Upon seeing an accident on the road, a driver moving at a speed of 72 km/h steps on the brake, imprinting a constant deceleration to the vehicle with a module equal to 2 m/s² until it stops completely. Determine:
a) The displacement suffered by the vehicle until its complete stop.
b) The amount of time required for the vehicle to come to a complete stop.
Resolution:
a) We can calculate the vehicle displacement using the Torricelli equation. Watch:

The exercise says that the vehicle's initial speed was 72 km/h. To start the calculation, we must transform this unit to meters per second (m/s), which is the unit of speed used in the international system of units (SI). For this, we divide this value by the factor 3,6, resulting in 20 m/s. In addition, the exercise informs you that the vehicle comes to a complete stop, so its final speed is 0. The vehicle deceleration being equal to 2 m/s², We have to:

b) We can calculate the time interval in which the movement occurred in two different ways: using the hourly position function or the hourly velocity function. However, the second option is the simplest, since the hourly function of the position is a 2nd degree equation. The hourly speed function is shown below:

Replacing the values provided in the exercise statement, we have:
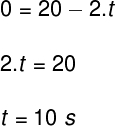
Therefore, the vehicle took 10 s until it came to a complete stop after seeing the accident on the track.
By Me. Rafael Helerbrock
Source: Brazil School - https://brasilescola.uol.com.br/fisica/equacao-torricelli.htm
