Equilateral triangle: area, perimeter, examples

O equilateral triangle is a special type of triangle. For this reason, all properties that apply to triangles are valid for it, but this type also has specific properties.

When one polygon it has only three sides, it is known as triangle. This geometric shape can be classified when comparing its sides. So a triangle can be scalene, when all sides are different;isosceles, when two sides are congruent; and equilateral, when the three sides are congruent.

The equilateral triangle has specific characteristics because of its equal measurements. There are even formulas for calculating area and perimeter that are efficient only for equilateral triangles

Read too: Pyramids - geometric figures whose side faces are formed by triangles

Properties of the equilateral triangle

A triangle is known as an equilateral when it has the measurement of the three congruent sides, thus, consequently, the your angles internal are also congruent. Since the sum of the interior angles of a triangle is always equal to 180º and the angles are equal, when we divide 180º by 3, we will arrive at angles of 60º. The internal angles of the equilateral triangle, therefore, always measure 60°.

instagram story viewer

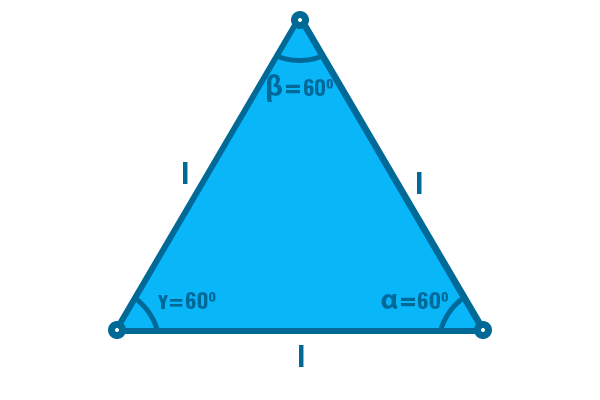
Because of these characteristics, the equilateral triangle has specific properties. if we trace the height of the equilateral triangle, it will also be bisector (line segment that divides the angle into two congruent parts) and average (straight line that connects the vertex to the midpoint of the opposite side).

When dividing the triangle as done in the previous image, the height of the triangle can be written as a function of the side, which can be demonstrated by both trigonometry how much by Pythagorean theorem.

The formula for calculating the height of an equilateral triangle is:

Read too:Median, bisector and height of a triangle

→ 1st demonstration:

In Pythagoras' theorem, it is shown that there is a relationship between the sides of a right triangle. The sum of the square of the legs is equal to the hypotenuse squared. The hypotenuse is the largest side opposite the 90° angle (in our case, the side that measures there), and the legs are the other two sides. So, we have to:

→ 2nd demonstration:

It is worth remembering two important facts about trigonometry. One of them is the sine of one angle and the other is the sine value of 60°.

The sine of any angle is given by the relationship between the opposite side and the hypotenuse of the right triangle:

It is also worth remembering the remarkable angles, which are the angles of 30º, 45º and 60º. In this case we will use the 60º angle, so it is important to point out that:

This makes it possible to demonstrate that height only depends on h. Look:

Regardless of the type of demonstration, you can see that the height (h) depends only on the value of the side to be calculated.

Perimeter of the equilateral triangle

Perimeter is the sum of all sides of a polygon. As the equilateral triangle is a regular polygon, i.e, has all three congruent sides, the calculation of your perimeter is very simple, it only depends on the measurement on the side there of an equilateral triangle. As it has all three sides with the same measure, we have to:

P = 3there

Example 1:

Calculate the perimeter of the equilateral triangle whose side measures 9 cm.

Resolution:

P = 3there

P = 3.9 = 27 cm

Example 2:

To fence a plot of land with 5 loops of wire, 450 meters of wire were needed. Knowing that the terrain is shaped like an equilateral triangle, what is the measurement of each of its sides?

Resolution:

We have as a given 5 times the perimeter and we want to find the value of the sides.

Therefore, we have to:

Also access: Prism area - calculation made from the flat geometric solids

equilateral triangle area

We understand that area of a triangle any is given by multiplication of base by height divided by two, but the equilateral triangle has a special formula for it, which is as follows: