Inverse matrix: what is it, how to find exercises

The concept of inverse matrix comes very close to the concept of the inverse of a number. Let's remember that the inverse of a number no is the number no^-1, where the product between the two is equal to the neutral element of the multiplication, that is, the number 1. Already the inverse of matrix M is matrix M^-1, where the product M · M^-1 is equal to the identity matrix I_no, which is nothing more than the neutral element of matrix multiplication.

In order for the matrix to have an inverse, it must be square and, moreover, its determinant must be different from zero, otherwise there will be no inverse. To find the inverse matrix, we use the matrix equation.

Read too: Triangular matrix — special type of square matrix

For a matrix to have an inverse, it must be square.

identity matrix

To understand what the inverse matrix is, it is first necessary to know the identity matrix. We know as an identity matrix the square matrix I_no where all elements of the main diagonal are equal to 1 and the other terms are equal to 0.

THE identity matrix is ​​the neutral element of multiplication between matrices., that is, given a headquarters M of order n, the product between matrix M and matrix I_no is equal to matrix M.

M · I_no = M

How to calculate the inverse matrix

To find the inverse matrix of M, it is necessary to solve a matrix equation:

 M · M^-1 = I_no

Example

Find the inverse matrix of M.

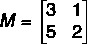
Since we don't know the inverse matrix, let's represent this matrix algebraically:

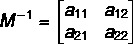
We know that the product between these matrices has to be equal to I₂:

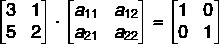
Now let's solve the matrix equation:

It is possible to separate the problem into two systems of equations. The first uses the first column of the matrix M ·M^-1 and the first column of the identity matrix. So, we have to:

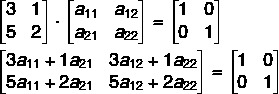
To solve the system, let's isolate the₂₁ in equation II and substitute in equation I.

Substituting in equation I, we have to:

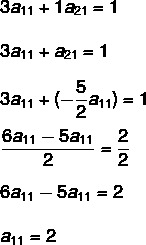
How do we find the value of a₁₁, then we'll find the value of a₂₁:

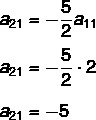
Knowing the value of a₂₁ and the₁₁, now we will find the value of the other terms by setting up the second system:

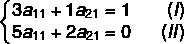
isolating the₂₂ in equation III, we have to:

3rd₁₂ + 1st₂₂ = 0

The₂₂ = – 3rd₁₂

Substituting in equation IV:

5th₁₂ + 2nd₂₂ =1

5th₁₂ + 2·( - 3rd₁₂) = 1

5th₁₂ – 6th₁₂ = 1

- a₁₂ = 1 ( – 1)

The₁₂ = – 1

Knowing the value of a₁₂, we will find the value of a₂₂ :

The₂₂ = – 3rd₁₂

The₂₂ = – 3 · ( – 1)

The₂₂ = 3

Now that we know all the terms of the matrix M^-1, it is possible to represent it:

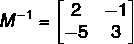
Read too: Addition and subtraction of matrices

Inverse Matrix Properties

There are properties that result from defining an inverse matrix.

• 1st property: the inverse of the matrix M^-1 is equal to matrix M. The inverse of an inverse matrix is ​​always the matrix itself, that is, (M^-1)^-1 = M, because we know that M^-1 · M = I_no, therefore M^-1 is the inverse of M and also M is the inverse of M^-1.
• 2nd property: the inverse of an identity matrix is ​​itself: I^-1 = I, because the product of the identity matrix by itself results in the identity matrix, that is, I_no · I_no = I_no.
• 3rd property: the inverse of product of two matrixare you is equal to the product of the inverses:

(M×H)^-1 = M^-1 · A^-1.

• 4th property: a square matrix has inverse if and only if its determinant is different from 0, that is, det(M) ≠ 0.

solved exercises

1) Given matrix A and matrix B, knowing that they are inverses, then the value of x+y is:

a) 2.

b) 1.

c) 0.

d) -1.

e) -2.

Resolution:

Alternative d.

Building the equation:

A · B = I 

By the second column, equaling the terms, we have to:

3x + 5y = 0 → (I)

2x + 4y = 1 → (II)

Isolating x into I:

Replacing in equation II, we have to:

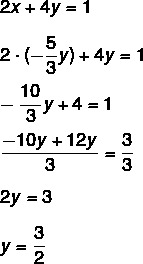
Knowing the value of y, we will find the value of x:

Now let's calculate x + y:

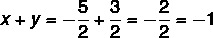
question 2

A matrix only has an inverse when its determinant is different from 0. Looking at the matrix below, what are x values ​​that make the matrix not support inverse?

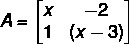
a) 0 and 1.

b) 1 and 2.

c) 2 and – 1.

d) 3 and 0.

e) – 3 and – 2.

Resolution:

Alternative b.

Calculating the determinant of A, we want values ​​where det(A) = 0.

det (A) = x ·(x – 3) – 1 · ( – 2)

det (A) = x² - 3x + 2

det (A) = x² - 3x + 2 = 0

solving the 2nd degree equation, We have to:

• a = 1
• b = – 3
• c = 2

Δ = b² - 4ac

Δ = (– 3) ² – 4·1·2

Δ= 9 – 8

Δ = 1

By Raul Rodrigues de Oliveira
Maths teacher

Source: Brazil School - https://brasilescola.uol.com.br/matematica/matriz-inversa.htm