At algebraic expressions are those mathematical expressions that have numbers and letters, also known as variables. We use letters to represent unknown values or even to analyze the behavior of the expression according to the value of this variable. Algebraic expressions are quite common in the study of equations and in writing formulas in Mathematics and related fields.
If the algebraic expression has a single algebraic term, it is known as monomial; when it has more than one, it is called polynomial. It is also possible to calculate algebraic operations, which are the operations between algebraic expressions.
Read too: Algebraic fractions - expressions that present at least one unknown in the denominator
What is an algebraic expression?
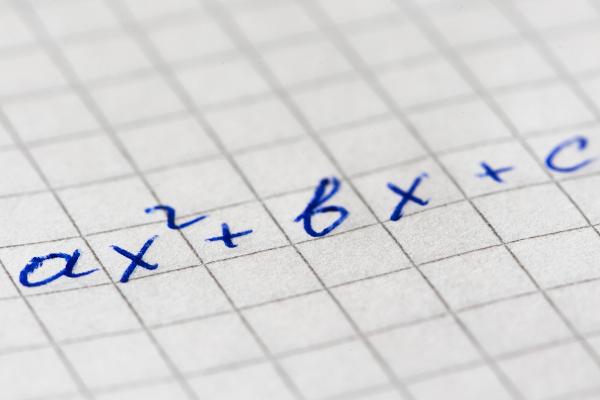
We define as algebraic expression a expression that contains letters and numbers, separated by basic math operations, like addition and multiplication. Algebraic expressions are of great importance for the most advanced study of Mathematics, making possible the calculation of unknown values in equations or even the study of functions. Let's look at some examples of algebraic expressions:
a) 2x²b + 4ay² + 2
b) 5m³n8
c) x² +2x - 3
Algebraic expressions are given particular names depending on how many algebraic terms they have.
monomials
An algebraic expression is known as a monomium when it has just an algebraic term. An algebraic term is one that has letters and numbers separated only by a multiplication between them.
A monomium is divided into two parts: o coefficient, which is the number that is multiplying the letter, and the literal part, which is the variable with its exponent.
Examples:
a) 2x³ → coefficient equals 2 and the literal part equals x³.
b) 4ab → coefficient equals 4 and the literal part equals ab.
c) m²n → coefficient is equal to 1 and the literal part is equal to m²n.
When the literal parts of two monomials are the same, they are known as similar monomials.
Examples:
a) 2x³ and 4x³ are similar.
b) 3ab² and -7ab² are similar.
c) 2mn and 3mn² no are similar.
d) 5y and 5x no are similar.
See too: Addition and subtraction of algebraic fractions – how to calculate?
Polynomials
When the algebraic expression has many algebraic terms, it is known as a polynomial. A polynomial is nothing more than the sum or difference between monomials. It is quite common to use polynomials in the study of equations and functions, or in the analytic geometry, to describe the equations of elements of geometry.
Examples:
a) 2x² + 2x + 3
b) 2ab - 4ab² + 2a - 4b + 1
c) 5mn - 3
d) 4y² + x³ – 4x + 8
Simplification of Algebraic Expressions
In an algebraic expression, when there are similar terms, it is possible to simplify this expression. through operations with the coefficients of similar terms.
Example:
5xy² + 10x – 3xy + 4x²y – 2x²y² + 5x – 3xy + 9xy² – 4x²y + y
For simplicity, let's identify similar terms, that is, terms that have the same literal part.
5xy²+ 10x– 3xy+ 4x²y – 2x²y² + 5x– 3xy+ 9xy² – 5x²y
We will perform the operations between similar terms, then:
5xy² + 9xy² = 14xy²
10x + 5x = 15x
-3xy – 3xy = -6xy
4x²y -5x²y = -1x²y= -x²y
The term -2x²y² has no term similar to it, so the simplified algebraic expression will be:
-2x²y² + 14xy² + 15x – 6xy -x²y
algebraic operations
Adding or subtracting algebraic expressions is nothing more than simplifying the expression, so it is only possible to operate with algebraic terms that are similar. In multiplication, however, it is necessary to use the distributive property between the terms, as shown in the following examples:
Addition example:
(2x² + 3xy - 5) + (3x² - xy + 2)
As it is an addition, we can simply remove the parentheses, without changing any of the terms:
2x² + 3xy - 5 + 3x² - xy + 2
Now let's simplify the expression:
5x² +2xy - 3
Subtraction example:
(2x² + 3xy - 5) - (3x² - xy + 2)
To remove the parentheses, it is necessary to invert the sign of each algebraic term in the second expression:
2x² + 3xy – 5 –3x² + xy – 2
Now let's simplify the expression:
– x² + 4xy – 7
Multiplication example:
(2x² + 3xy - 5) (3x² - xy + 2)
Applying the distributive property, we will find:
6x4 – 2x³y + 4x² + 9x³y – 3x²y² +6xy – 15x² – 5xy + 10
Now let's simplify the expression:
6x4 + 7x³y – 11x² –3x²y² + xy + 10
Also access: How to simplify algebraic fractions?
Numerical value of algebraic expressions
When we know the variable value of an algebraic expression, it is possible to find its numerical value. The numerical value of the algebraic expression is nothing more than the final result when we replace the variable with a value.
Example:
Given the expression x³ + 4x² + 3x – 5, what is the numeric value of the expression when x = 2.
To calculate the value of the expression, let's replace x with 2.
2³ + 4 · 2² + 3 · 2 – 5
8 + 4 · 4 + 6 – 5
8 + 16 + 6 – 5
30 – 5
25
solved exercises
Question 1 - The algebraic expression that represents the perimeter of the following rectangle is:

A) 5x – 5
B) 10x – 10
C) 5x + 5
D) 8x - 6
E) 3x - 2
Resolution
Alternative B.
To calculate the perimeter, let's add the four sides together. Knowing that the parallel sides are the same, we have to:
P = 2(2x - 4) + 2 (3x - 1)
P = 4x – 8 + 6x – 2
P = 10x – 10
Question 2 - (Enem 2012) A rectangular fabric lining has on its label the information that it will shrink after the first wash, keeping, however, its shape. The following figure shows the original ceiling measurements and shrinkage size (x) in length and (y) in width. The algebraic expression that represents the area of the ceiling after being washed is (5 – x) (3 – y).

Under these conditions, the lost area of the lining, after the first wash, will be expressed by:
A) 2xy
B) 15 - 3x
C) 15 - 5y
D) -5y – 3x
E) 5y + 3x – xy
Resolution
Alternative E.
To calculate the area of a rectangle, we calculate the area by finding the product between the base and height of the rectangle. Analyzing the missing part of the ceiling, it is possible to divide it into two rectangles, but there is a region that belongs to the two rectangles, so we will have to subtract the area from this region.
The largest rectangle has base 5 and height y, so its area is given by 5y. The other triangle has base x and height 3, so its area is given by 3x. The region that belongs to the two rectangles simultaneously has base x and height y, so since it's being counted in the two rectangles, let's subtract it from the sum of the areas. Thus, the lost area is given by the algebraic expression:
5y + 3x - xy
By Raul Rodrigues Oliveira
Maths teacher
Source: Brazil School - https://brasilescola.uol.com.br/matematica/expressao-algebrica.htm


