We know that the basic elements of a triangle are: vertices, sides and angles, but they are not the only ones. In a triangle we identify other elements such as median, bisector and height.
Vertices, sides and angles.
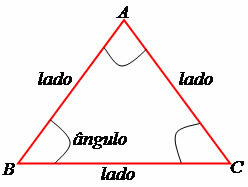
Vertices: A, B and C
Sides: AB, BC and AC
Angles: A, B and C
median
Median is a segment that divides the bases of the triangle into two equal parts. Thus, we have that median is a line segment that originates from one of the vertices of the triangle and ends at the midpoint of the opposite side of the vertex. Look at the picture:

A, B and C are the vertices of ΔABC.
M base midpoint BC, thus BM = MC.
AM line segment with ends at vertex A and at midpoint M, so in this example we can say that segment AM is the median of ΔABC.
Bisector
Bisector is also a line segment originating from one of the triangle's vertices with the other end on the opposite side of that vertex. Since it divides the angle corresponding to the vertex in half. See the example:

AS is a line segment that has divided angle  into two equal parts.
Height
We find the measure of the height of a triangle through a line segment originating from one of the vertices and perpendicular (forms a 90º angle) to the opposite side.
Height in Acute Triangle

Segment AH originates from vertex A and is perpendicular to side BC, so AH is the height of ΔABC.
height in right triangle

In this triangle, the segment EF represents the height of the ΔEFG as it is perpendicular to the side FG.
height in obtuse triangle
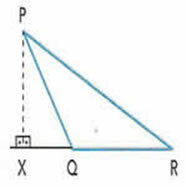
The RQ base was extended forming the RX segment. From vertex P to point x we form a straight line perpendicular to RX, so PX is the height of ΔPQR.
by Mark Noah
Graduated in Mathematics
Brazil School Team
triangle - Math - Brazil School
Source: Brazil School - https://brasilescola.uol.com.br/matematica/mediana-bissetriz-altura-um-triangulo.htm

