O set of Natural Numbers is a numerical set formed by 0, 1, 2, 3, 4, 5, … We say that this set is positively infinite, as there are no negative, decimal or fractional numbers. This set is represented by the symbol.
We use the following notation to represent the set of Natural Numbers:
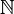= {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, …}
We can say that within the set of natural numbers there are subsets, such as:
-
Set of non-zero natural numbers:
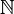* = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, …}
-
Set of even natural numbers:
P = {0, 2, 4, 6, 8, 10, …}
-
Set of odd natural numbers:
I = {1, 3, 5, 7, 9, 11, ...}
We can say that the sets of natural numbers non-zero, even numbers, and odd numbers are contained in the set of natural numbers, since all elements of each of these subsets belong to .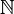
The set of natural numbers allows the application of all mathematical operations, with only a few caveats in some operations:
Addition: does every natural number added to another natural number also result in some natural number, ie, let a, b, and c?
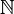, a + b = c ? 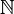.Subtraction: a natural number subtracted from another natural number results in a natural number, as long as the first number is greater than the second number, that is, is a, b, and c?
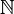, such that a > b, then, a - b = c ? 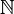.Multiplication: is the product of two natural numbers always a natural number, that is, let a, b, and c?
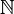, then, The. b = c ? 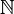.Division: Will the quotient of two natural numbers be a natural number since the dividend is a multiple of the divisor, that is, be a, b, and c?
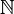, then a: b = c ? 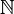; if and only if The= b. no, where n? 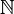.Potentiation: will the power of a natural number always be natural as long as the exponent is also natural, that is, is a, b and c?
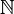, then TheB = c ? 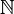; if and only if B? 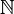.Radiation: the root of a natural number will also be natural since the radicand is the power of some natural number.
By Amanda Gonçalves
Graduated in Mathematics
Source: Brazil School - https://brasilescola.uol.com.br/o-que-e/matematica/o-que-e-conjunto-dos-numeros-naturais.htm
