We can classify a linear system in three ways:
• SPD – Possible system determined; there is only one solution set;
• SPI – Indeterminate impossible system; there are numerous solution sets;
• SI – Impossible system; it is not possible to determine a solution set.
However, many times we are only able to classify the systems when we are in the final parts of solving each one, or even through the calculation of the determinant. However, when we carry out the scaling of a linear system, we walk with great strides towards obtaining the solution set and classification of the linear system.
This happens because the linear scaled system has a fast way to obtain the values of the unknowns, since it tries to write each equation with a smaller number of unknowns.
To classify the linear system that is scaled, it is enough to analyze two elements.
1.The last line of the system that is fully scaled;
2.The number of unknowns compared to the number of equations given in the system.
At the first In this case, the following situations may occur:
• A first degree equation with an unknown, the system will be SPD. Example: 2x=4; 3y=12; z=1
• Equality without unknowns: there are two possibilities, equalities that are true (0=0; 1=1;…) and false equals (1 = 0; 2 = 8). When we have true equals, we will classify our system as SPI, while with false equations our system will be impossible (SI).
• Equation with a null coefficient. In this case there are also two possibilities, one in which the independent term is null and one in which it is not.
• When we have an equation with null coefficients and null independent term, we will classify our system as SPI, because we will have infinite values that will satisfy this equation, check this out: 0.t = 0
Whichever value is placed in the unknown t, the result will be zero, since any number multiplied by zero is zero. In this case, we say that the unknown t is a free unknown, as it can take any value, therefore we attribute to it a representation of any value, which in mathematics is done through a letter.
• When we have an equation of null coefficients and independent term different from zero, we will classify our system as SI, because for any value that t assumes, it will never be equal to desired value. See an example:
Do not stop now... There's more after the advertising ;)
0.t = 5
Whatever the value of t, the result will always be zero, that is, this equation will always be of the form (0 = 5), for whatever the value of the unknown t. For this reason, we say that a system that has an equation in this way is an unsolvable, impossible system.
At the second In this case, when the number of unknowns is greater than the number of equations, we will never have a possible and determined system, leaving us only the other two possibilities. These possibilities can be obtained by carrying out the comparison mentioned in the previous topics. Let's look at two examples that cover these possibilities:

Note that none of the systems have been scaled.
Let's schedule the first system.
Multiplying the first equation and adding it to the second, we have the following system:
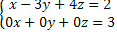
Analyzing the last equation we see that it is an impossible system, as we can never find a value that satisfies the equation.
Scaling the second system:

Looking at the last equation, it is an indeterminate possible system.
By Gabriel Alessandro de Oliveira
Graduated in Mathematics
Brazil School Team
Would you like to reference this text in a school or academic work? Look:
OLIVEIRA, Gabriel Alessandro de. "Scoring the solutions of a linear scaled system"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/classificando-as-solucoes-um-sistema-linear-escalonado.htm. Accessed on June 29, 2021.


