To the operations with sets they are union, intersection and difference. The result of each of these operations is a new set. To indicate the union between sets, we use the symbol ∪; for the intersection, the symbol ∩; and for the difference, the symbol of subtraction\(-\). In the case of a difference, it is essential to observe the order in which the operation will be carried out. In other words, if A and B are sets, then the difference between A and B is different from the difference between B and A.
Read too: Venn diagram — geometric representation of sets and operations between them
Summary of operations with sets
Operations with sets are: union, intersection and difference.
The union (or meeting) of sets A and B is the set A ∪ B, formed by the elements that belong to A or belong to B.
\(A∪B=\{x; x∈A\ or\ x∈B\}\)
The intersection of sets A and B is the set A ∩ B, formed by the elements that belong to A and belong to B.
\(A∩B=\{x; x∈A\ and\ x∈B\}\)
The difference between sets A and B is the set A – B, formed by the elements that belong to A and do not belong to B.
\(A -B =\{x; x∈A\ e\ x ∉B\}\)
If U (known as the universe set) is a set that contains all sets in a given context, then the difference U – A, with A ⊂ U, is called the complement of A. The complement of A is formed by elements that do not belong to A and is represented by Aw.
\(A^c=U-A=\{x; x∉A\}\)
Video lesson on operations with sets
What are the three operations with sets?
The three operations with sets are: union, intersection and difference.
Union of sets
The union (or meeting) of sets A and B is the set A ∪ B (read “The union B”). This set is made up of all the elements that belong to set A or belong to set B, that is, the elements that belong to at least one of the sets.
Representing the elements of A ∪ B by x, we write
\(A∪B=\{x; x∈A\ or\ x∈B\}\)
In the image below, the orange region is the set A ∪B.

It seems difficult? Let's look at two examples!
Example 1:
What is the set A ∪ B, if A = {7, 8} and B = {12, 15}?
The set A ∪ B is formed by the elements that belong to A or belong to B. Since elements 7 and 8 belong to the set A, then both of them must belong to the set A ∪ B. Furthermore, as elements 12 and 15 belong to the set B, then both must belong to the set A ∪ B.
Therefore,
A ∪ B={7, 8, 12, 15}
Note that each of the elements of A∪B belongs to either set A or set B.
Example 2:
Consider the sets A = {2, 5, 9} and B = {1, 9}. What is the set A ∪ B?
Since elements 2, 5 and 9 belong to the set A, then they must all belong to the set A∪B. Furthermore, since elements 1 and 9 belong to the set B, then they must all belong to the set A ∪ B.
Note that we mentioned 9 twice, as this element belongs to set A and set B. Saying that “the set A ∪ B is formed by the elements that belong to A or belong to B” does not exclude elements that simultaneously belong to sets A and B.
So, in this example, we have
A ∪ B={1, 2, 5, 9}
Note that we write element 9 only once.
Intersection of sets
The intersection of sets A and B is the set A ∩ B (read “The intersection B”). This set is made up of all the elements that belong to set A It is belong to set B. In other words, A ∩ B is composed of the common elements of sets A and B.
Indicating the elements of A ∩ B by x, we write
\(A∩B=\{x; x∈A\ and\ x∈B\}\)
In the image below, the orange region is the set A ∩B.

Let's solve two examples about the intersection of sets!
Example 1:
Consider A = {-1, 6, 13} and B = {0, 1, 6, 13}. What is the set A ∩ B?
The set A ∩ B is formed by all the elements that belong to the set A It is belong to set B. Note that elements 6 and 13 belong simultaneously to sets A and B.
Like this,
A ∩ B={6, 13}
Example 2:
What is the intersection between the sets A = {0,4} and \(B={-3,\frac{1}2,5,16,44}\)?
Note that there is no element in common between sets A and B. Thus, the intersection is a set without elements, that is, an empty set.
Therefore,
\(\)A ∩ B={ } = ∅
Difference between sets
The difference between sets A and B is the set A – B (read “difference between A and B”). This set consists of all elements that belong to set A and do not belong to set B.
Portraying the elements of A – B by x, we write
\(A-B=\{x; x∈A\ and\ x∉B\}\)
In the image below, the orange region is the setA – B.
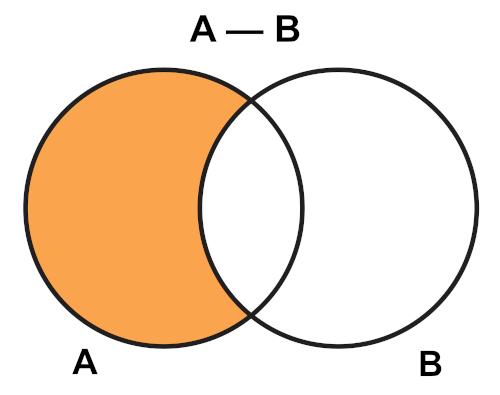
Attention: the difference between sets A and B is not the difference between sets B and A, because B – A is formed by all the elements that belong to set B and do not belong to set A.
Consider the two examples below about difference between sets.
Example 1:
If A = {-7, 2, 100} and B = {2, 50}, then what is the set A – B? What about the set B – A?
The setA-B is made up of all the elements that belong to the set A It isno belong to set B. Note that 2 is the only element in set A that also belongs to set B. Thus, 2 does not belong to the set A – B.
Therefore,
A – B = {-7, 100}
Furthermore, the set B – A is formed by all the elements that belong to the set B It isno belong to set A. Therefore,
B – A = {50}
Example 2:
What is the difference between the set A = {–4, 0} and the set B = {–3}?
Note that none of the elements of A belong to B. Thus, the difference A – B is the set A itself.
\(A - B = \{-4.0\} = A\)
Observation: Consider that U (called the universe set) is a set that contains all other sets in a given situation. Like this, the difference U–A, with A⊂U, is a set called complementary to A and portrayed as \(B.C\).
\(A^c=U-A=\{x; x∉A\}\)
In the following image, the rectangle is the universe set and the orange region is the universe set \(B.C\).

Know more: Step by step how to do a division
Solved exercises on set operations
Question 1
Consider the sets A = {–12, –5, 3} and B = {–10, 0, 3, 7} and classify each statement below as T (true) or F (false).
I. A ∪ B = {–12, –10, –5, 3, 7}
II. A ∩ B = {3}
III. A – B = {–12, –5}
The correct order, from top to bottom, is
A) V-V-V
B) F-V-V
C) V-F-V
D) F-F-V
E) F-F-F
Resolution
I. False.
Element 0 must belong to the union of A and B, since 0 ∈ B. Thus, A ∪ B = {–12, –10, –5, 0, 3, 7}
II. True.
III. True.
Alternative B.
Question 2
Consider A = {4, 5}, B = {6,7} and C = {7,8}. Then, the set A ∪ B ∩ C is
A) {7}.
B) {8}.
C) {7, 8}.
D) {6,7,8}.
E) {4, 5, 6, 7, 8}.
Resolution
Note that A ∪ B = {4, 5, 6, 7}. Therefore, the set A ∪ B ∩ C is the intersection between A ∪ B = {4, 5, 6, 7} and C = {7,8}. Soon,
A ∪ B ∩ C = {7}
Alternative A.
Sources
LIMA, Elon L.. Analysis Course. 7 ed. Rio de Janeiro: IMPA, 1992. v.1.
LIMA, Elon L. et al. High School Mathematics. 11. ed. Mathematics Teacher Collection. Rio de Janeiro: SBM, 2016. v.1.



