O Venn diagram is a way we use to represent the numerical sets which allows us to better visualize the elements of the sets and the operations between them (union, intersection and difference).
Read too: Numerical sequence — a set formed by numbers represented in an order
What is the Venn diagram?
The Venn diagram is a way of representing the elements of one or more sets. To make this representation, we use a closed geometric shape and write the elements of the set within this geometric shape. The Venn diagram makes it easier to visualize operations between sets.
Representations in the Venn diagram
To represent the elements of a set in the Venn diagram, we place the elements of the set inside the closed region.
→ Representation of a set in the Venn diagram
See below a representation of the elements of set A: {0, 1, 2, 5, 9, 10} in the Venn diagram.

→ Representation of two sets in the Venn diagram
To represent two sets in the diagram, we first analyze whether they have elements in common or not. In each of these cases, the way of representing is different.
◦ Representation of two sets that have elements in common
We want to represent the set A: {0, 1, 2, 5, 9, 10} and the set B: {0, 3, 4, 7, 9, 12}. Note that these sets have elements in common. These common elements are known as intersection and are the elements that will belong to both diagrams.. The common elements in these sets are {0, 9}. Then, we represent these sets as follows:

◦ Representation of two sets that have no elements in common
We want to represent the set A: {0, 1, 2, 5, 9, 10} and the set B: {3, 4, 6, 7, 12}. When sets have no elements in common, they are known as disjoint sets. Its representation in the Venn diagram is done as follows:

Operations between sets
The operations between sets are union, intersection and difference. We can use the Venn diagram to solve these operations.
→ Union of sets
The union between two sets is the union of all elements that belong to any of these sets. To represent the union between sets A and B, we use the symbol ∪ between the letters that represent the sets, that is, A∪B (read: The union with B).

Example:
Consider the sets A: {0, 1, 2, 5, 9, 10} and B: {0, 3, 4, 9, 11, 12}. The union of these sets is the set A∪B: {0, 1, 2, 3, 4, 5, 9, 10, 11, 12}.

→ Intersection of sets
The intersection of two sets is formed by elements that belong to both sets at the same time. The intersection symbol is ∩, so to represent the intersection between two sets we write A∩B (read: The intersection with B).

The intersection of sets in the Venn diagram is represented by the elements that belong to both the region that delimits set A and the region that delimits set B.
Example:
Consider the sets A: {0, 1, 2, 5, 9, 10} and B: {0, 3, 4, 9, 11, 12}. The intersection of these sets is the set A∩B: {0, 9}.

→ Difference between sets
The difference between two sets is represented by A – B. The difference is composed of elements that belong to one of the sets and do not belong to the other. For example, in the difference between sets A – B, we find the set formed by elements that belong only to set A, that is, they belong to set A but do not belong to set B.
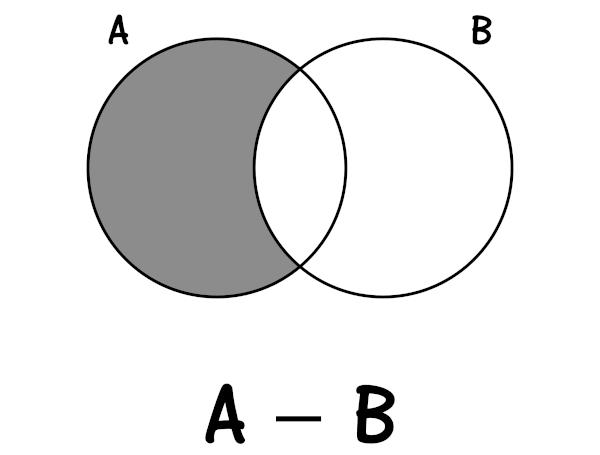
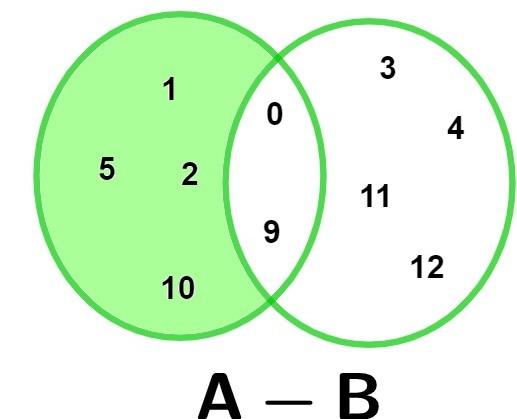
Example:
Consider the sets A: {0, 1, 2, 5, 9, 10} and B: {0, 3, 4, 9, 11, 12}. The difference A – B is the set A – B = {1, 2, 5, 10}, which are the elements that belong to set A but do not belong to set B.
Also know: Operations with fractions — how to do it?
Solved exercises on Venn diagram
Question 1
Analyze the Venn diagram represented in the following image:
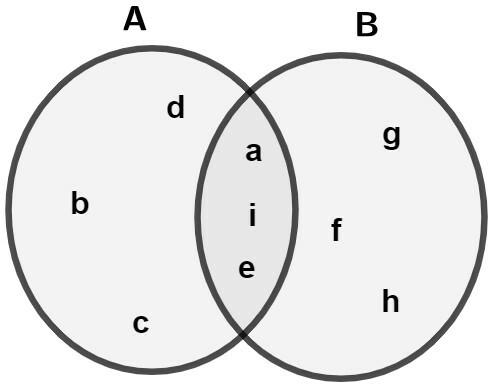
The elements belonging to the set B – A are:
A) {d, b, c, f, g, h}
B) {a, i, e}
C) {d, b, c}
D) {f, g, h}
E) {a, b, c, d, e, f, g, h, e, i}
Resolution:
Alternative D
We want the elements that belong only to set B. They are: {f, g, h}.
Question 2
Analyze the following diagram:

The highlighted region is:
A) The union between the two sets
B) The difference between the two sets
C) The intersection between the two sets
D) The complement of the first set.
Resolution:
Alternative C
The region that belongs to both sets at the same time is known as intersection.



