Study about quadrilaterals with this list of exercises that we have prepared for you. Clear your doubts with the answers explained step by step.
question 1
The quadrilateral below is a parallelogram. Determine the angle formed between the angle bisector x and the 6 m segment.

Answer: 75°.
Analyzing the lengths of the sides we can complete the missing measurements in the image.
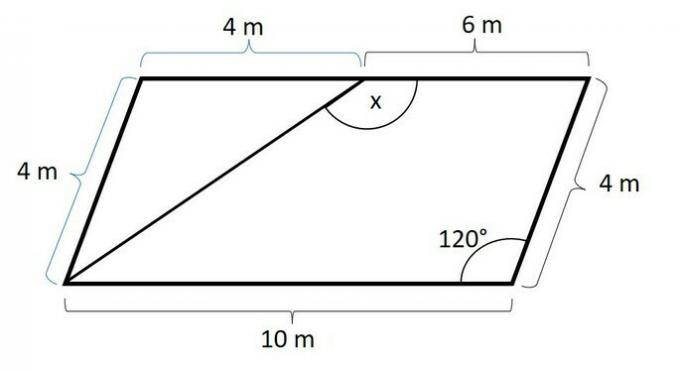
Since it is a parallelogram, the opposite sides are equal.
Angles at opposite vertices are equal.
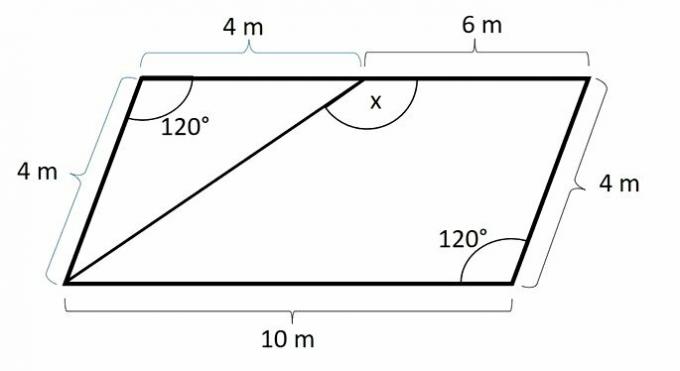
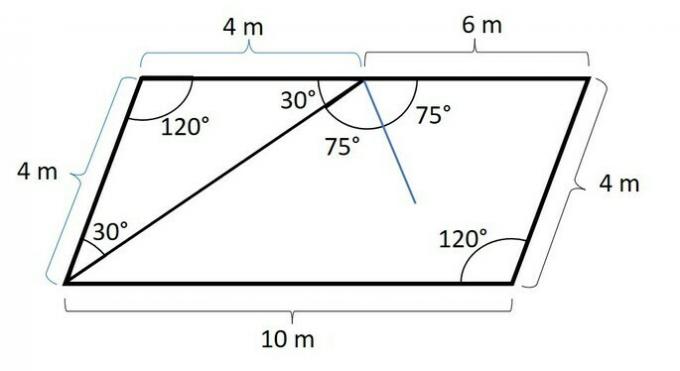
The triangle formed by two sides of 4 m is isosceles, so the base angles are equal. Since the sum of the interior angles of a triangle is equal to 180°, that leaves:
180° - 120° = 60°
These 60° are distributed equally between the two base angles, so:

The angle x together with the 30° angle form a straight angle, of 180°, so the angle x has:
x = 180° - 30° = 150°
Conclusion
Since the bisector is the ray that divides an angle in half, the angle between the bisector and the 6 m segment is 75°.
question 2
In the figure below, the horizontal lines are parallel and equidistant from each other. Determine the sum of the measures of the horizontal segments.

Answer: 90 m.
To determine the sum we need the lengths of the three inner segments of the trapezoid.
The mean base can be determined by an arithmetic mean:
The central segment is 18 m. Repeating the procedure for the upper inner segment:
For the lower inner segment:
So the sum of the parallel segments is:
14 + 16 + 18 + 20 + 22 = 90m
question 3
Find the values of x, y, and w in the isosceles trapezoid below.
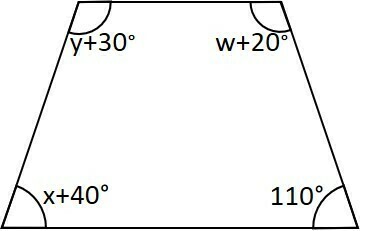
Response:
Since the trapezoid is isosceles, the base angles are equal.
At the angles of the minor base:
We also have that the sum of the four interior angles of a quadrilateral is equal to 360°.
To determine the value of y, we substitute the value of w in the previous equation.
Like this:
x = 70 degrees, w = 50 degrees and y = 40 degrees.
question 4
(MACKENZIE)
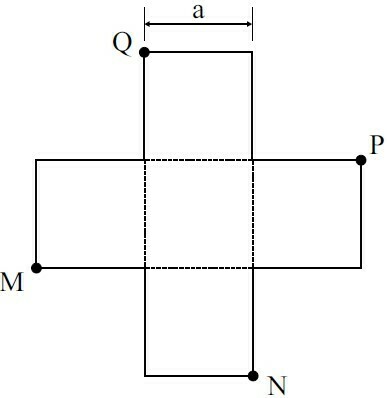
The figure above is formed by squares of sides a.
The area of the convex quadrilateral with vertices M, N, P and Q is
The)
B)
w)
d)
It is)
As the figure is formed by squares, we can determine the following triangle:
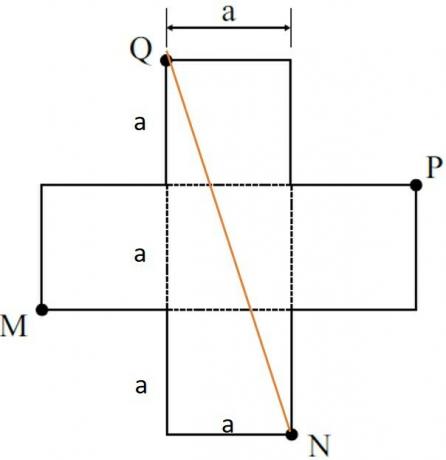
Thus, the diagonal of the square MNPQ is equal to the hypotenuse of the right triangle with height 3a and base a.
Using the Pythagorean Theorem:
The measure of QN is also the hypotenuse of the square MNPQ. Using once again the Pythagorean Theorem and naming the side of the square l, we have:
Substituting the value of QN² obtained earlier:
Since the area of the square is obtained by l², is the measure of the area of the square MNPQ.
question 5
(Enem 2017) A manufacturer recommends that, for each m2 of the environment to be air-conditioned, 800 BTUh are required, provided there are up to two people in the environment. To this number must be added 600 BTUh for each additional person, and also for each heat-emitting electronic device in the environment. Below are the five appliance options from this manufacturer and their respective thermal capacities:
Type I: 10 500 BTUh
Type II: 11,000 BTUh
Type III: 11 500 BTUh
Type IV: 12,000 BTUh
Type V: 12 500 BTUh
The supervisor of a laboratory needs to buy a device to air-condition the environment. It will house two people plus a centrifuge that emits heat. The laboratory has the shape of a rectangular trapeze, with the measurements shown in the figure.
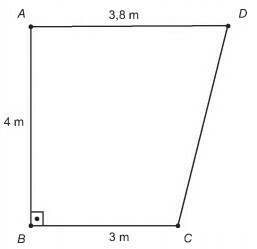
To save energy, the supervisor should choose the device with the lowest thermal capacity that meets the needs of the laboratory and the manufacturer's recommendations.
The supervisor's choice will fall on the device of the type
there.
b) II.
c)III.
d) IV.
e) v.
We start by calculating the area of the trapezoid.
Multiplying by 800 BTUh
13.6 x 800 = 10 880
As in addition to the two people there will also be a device that emits heat, according to the manufacturer, we must add 600 BTUh.
10 880 + 600 = 12480 BTUh
Therefore, the supervisor must choose the number V.
question 6
(Naval College) Given a convex quadrilateral in which the diagonals are perpendicular, analyze the statements below.
I - A quadrilateral thus formed will always be a square.
II - A quadrilateral thus formed will always be a rhombus.
III- At least one of the diagonals of a quadrilateral thus formed divides this quadrilateral into two isosceles triangles.
Tick the correct option.
a) Only statement I is true.
b) Only statement II is true.
c) Only statement III is true.
d) Only statements II and III are true.
e) Only statements I, II and III are true.
I - WRONG. There is a possibility that it is a rhombus.
II - WRONG. There is a possibility that it is a square.
III - CORRECT. Whether a square or a rhombus, a diagonal always divides the polygon into two isosceles triangles, as the characteristic of these polygons is that all sides have the same measure.
question 7
(UECE) The points M, N, O and P are the midpoints of the sides XY, YW, WZ and ZX of the square XYWZ. Segments YP and ZM intersect at point U and segments OY and ZN intersect at point V. If the length of the side of the square XYWZ is 12 m then the length, in m2, of the area of the quadrilateral ZUYV is
a) 36.
b) 60.
c) 48.
d) 72.
The situation described in the statement can be described as:

The figure formed is a rhombus and its area can be determined as:
The larger diagonal of the rhombus is also the diagonal of the square which can be determined by the Pythagorean theorem.
The smaller diagonal will be one third of the larger diagonal. Substituting into the area formula, we get:
Learn more at:
- Quadrilaterals: what they are, types, examples, area and perimeter
- What is a Parallelogram?
- trapeze
- Areas of Plane Figures
- Plane Figures Area: Solved and Commented Exercises
ASTH, Rafael. Exercises on quadrilaterals with explained answers.All Matter, [n.d.]. Available in: https://www.todamateria.com.br/exercicios-sobre-quadrilateros/. Access at:
See too
- quadrilaterals
- Exercises on triangles explained
- Exercises on polygons
- Area and perimeter exercises
- Area of Plane Figures - Exercises
- parallelogram
- Similarity of triangles: commented and solved exercises
- Areas of Plane Figures