A static and the field of Classical Mechanics responsible for studying systems of particles or rigid bodies in a state of equilibrium. In this area we study concepts such as the center of mass, torque, angular momentum, lever and balance.
Read too: Kinematics — area of Mechanics that studies the motion of bodies
summary about static
- The study of statics makes possible the construction and stability of buildings, bridges, automobiles, monuments, seesaws and much more.
- In statics, the concepts and applications of center of mass, balance, lever, torque, angular momentum are studied.
- The center of mass is calculated through the arithmetic mean of the mass of the particles and their positions in the system.
- Torque is calculated as the product of the force produced, the lever arm and the angle between the distance and the force.
- Angular momentum is calculated as the product of the object's distance from the axis of rotation, the linear momentum, and the angle between the distance and the linear momentum.
What does statics study?
The static studies rigid bodies or particles at rest, being static, because their forces and moments are canceling each other out in all directions, provoking the balance, with
this we can determine the internal forces that are on this system.
What is static for?
The study of statics is widely applied in the construction of bridges, buildings, houses, furniture, automobiles, doors, windows, finally, everything that needs balance. O study of levers allows you to understand and manufacture wheelbarrows, hammers, nutcrackers, dough hooks, fishing rods, seesaws and much more. In addition, the study of angular momentum makes it possible to improve the turns of skaters, bicycle wheels and swivel chairs.
See too: What is the concept of strength?
Important static concepts
- Center of mass: It is the point at which all the mass of a physical system or particle accumulates. It is not always in the body, as in the case of a ring, in which its
- center of mass is at the center, where there is no material. To learn more about this concept, click here.
- Balance: is the situation in which the sum of all forces and moments on a body is zero, keeping the body unchanged.
-
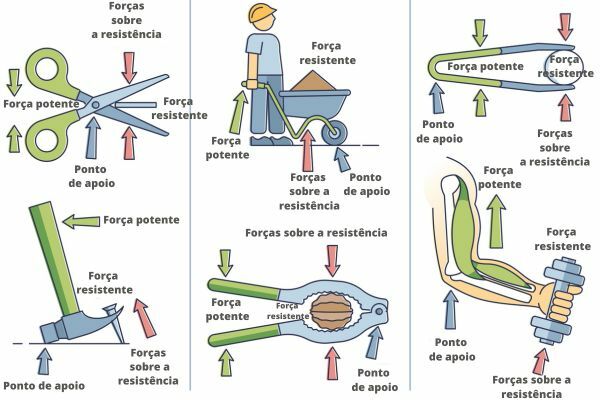
Lever: It is a simple machine capable of simplifying the execution of a task, and can be interfixed, interpotent and inter-resistant.
- A leverinterfix it has the support point between the potent force and the resistant force, as is the case of scissors, pliers, seesaw and hammer.
- A leverinterresistant it has the resistant force between the potent force and the fulcrum, as is the case with the nutcracker, bottle opener, wheelbarrow.
- A leverinterpotent it has the powerful force between the resistant force and the fulcrum, as is the case with tweezers, nail clippers, some bodybuilding exercises.
- Torque: also called moment of force, is a physical quantity that occurs when we apply a force on a body capable of rotating, turning, like opening a revolving door. Learn more about this concept by clicking here.
- Angular moment: It is a physical quantity that informs about the amount of movement of bodies that are rotating, rotating or making curves.
Main formulas of statics
→ Center of mass formulas
\(X_{CM}=\frac{m_1\cdot x_1+m_2\cdot x_2 +m_3\cdot x_3}{m_1+m_2+m_3 }\)
It is
\(Y_{CM}=\frac{m_1\cdot y_1+m_2\cdot y_2 +m_3\cdot y_3}{m_1+m_2+m_3 }\)
xcm is the position of the center of mass of the particle system on the horizontal axis.
ycm is the position of the center of mass of the particle system on the vertical axis.
m1, m2 It is m3 are the masses of the particles.
x1, x2 It is x3 are the positions of the particles on the horizontal axis.
y1, y2 It is y3 are the positions of the particles on the vertical axis.
→ Lever formula
\(F_p\cdot d_p=F_r\cdot d_r\)
FP is the potent force, measured in Newton [N].
dP is the distance of the potent force, measured in meters [m].
Fr is the resisting force, measured in Newton [N].
dr is the distance of the resisting force, measured in meters [m].
→ Torque formulas
\(τ=r\cdot F\cdot sinθ\)
τ is the torque produced, measured in N∙m.
r is the distance from the axis of rotation, also called the lever arm, measured in meters [m].
F is the force produced, measured in Newton [No].
θ is the angle between the distance and the force, measured in degrees [°].
When the angle is 90º, the torque formula can be represented by:
\(τ=r\cdot F\)
τ is the torque produced, measured in [N∙m].
r is the distance from the axis of rotation, also called the lever arm, measured in meters [m].
F is the force produced, measured in Newton [No].
→ Angular Momentum Formula
\(L=r\cdot p\cdot sinθ\)
L is the angular momentum, measured in [kg∙m2/s].
r is the distance between the object and the axis of rotation or radius, measured in meters [m].
P is the linear momentum, measured in [kg∙m/s].
θ is the angle between the r It is Q, measured in degrees [°].
Know more: Hydrostatics — branch of Physics that studies fluids under conditions of static equilibrium
Solved exercises on statics
01) (UFRRJ-RJ) In the figure below, suppose the boy is pushing the door with a force Fm = 5 N, acting at a distance of 2 m from the hinges (axis of rotation), and that the man exerts a force FH = 80 N, at a distance of 10 cm from the axis of rotation.

Under these conditions, it can be stated that:
a) the door would be turning in the direction of being closed.
b) the door would be turning in the direction of being opened.
c) the door does not rotate in any direction.
d) the value of the moment applied to the door by the man is greater than the value of the moment applied by the boy.
e) the door would be turning in the direction of being closed, because the mass of the man is greater than the mass of the boy.
Resolution:
Alternative B. The door would be turning in the direction of being opened. To do this, just calculate the torque of the man, through the formula:
\(τ_h=r\cdot F\)
\(τ_h=0.1\cdot80\)
\(τ_h=8N\cdot m\)
And the boy torque:
\(τ_m=r\cdot F\)
\(τ_m=2\cdot 5\)
\(τ_m=10N\cdot m\)
So, you can see that the boy's torque is greater than the man's torque, so the door is opening.
02) (Enem) In an experiment, a teacher took to the classroom a bag of rice, a triangular piece of wood and a cylindrical and homogeneous iron bar. He proposed that they measure the mass of the bar using these objects. For this, the students made marks on the bar, dividing it into eight equal parts, and then supporting it on the triangular base, with the bag of rice hanging from one of its ends, until equilibrium is reached.

In this situation, what was the mass of the bar obtained by the students?
a) 3.00 kg
b) 3.75 kg
c) 5.00 kg
d) 6.00 kg
e) 15.00 kg
Resolution:
E alternative. We will calculate the mass of the bar obtained by the students, through the formula of the lever, in which we compare the potent force with the resistant force:
\(F_p\cdot d_p=F_r\cdot d_r\)
The force that the rice exerts is what resists the movement of the bar, so:
\(F_p\cdot d_p=F_{rice}\cdot d_{rice}\)
The force acting on the rice and the potent force is the weight force, so:
\(P_p\cdot d_p=P_{rice}\cdot d_{rice}\)
\(m_pg\cdot d_p=m_{rice}\cdot g\cdot d_{rice}\)
\(m_p\cdot10\cdot1=5\cdot10\cdot3\)
\(m_p\cdot10=150\)
\(m_p=\frac{150}{10}\)
\(m_p=15 kg\)
Sources
HALLIDAY, David; RESNICK, Robert; WALKER, Jearl. Fundamentals of Physics: Mechanics.8. ed. Rio de Janeiro, RJ: LTC, 2009.
NUSSENZVEIG, Herch Moyses. basic physics course: Mechanics (vol. 1). 5 ed. So Paulo: Blucher, 2015.
