One high school function is the one that can be written in the form f(x) = ax2 + bx + c. All high school function is geometrically represented by a parable, which is a geometric figure flat. The parables connected to functions of the second degree have a maximum point or a minimum point. The biggest candidate for one of these points is called vertex of the parabola.
Getting the vertex coordinates
At vertex coordinates can be obtained in two ways. The first uses one of the following formulas:
xv = - B
2nd
yv = – Δ
4th
In these formulas, xv and yv are the coordinatesofvertex of the function of the seconddegree, that is, V(xvyv).
The second way to find the coordinates of the vertex is as follows: suppose x1 and x2 be the roots of a function of the seconddegree, the midpoint between the roots will be the x coordinate of the vertex. Knowing this, just find the image of this value through the occupation analyzed. So, given the x roots1 and x2 of a function f(x) = ax2 + bx + c, we have:
xv = x1 + x2
2
yv = f(xv) = axv2 + bxv + c
This is the second technique used to demonstrate the given formulas.
Demonstration of formulas
Given a function of the second degree any f (x) = ax2 + bx + c, with roots x1 and x2, we can find the x coordinatev calculating the average between these roots. To do this, remember that:
x1 = – b + √Δ
2nd
x2 = - B - √Δ
2nd
Therefore:
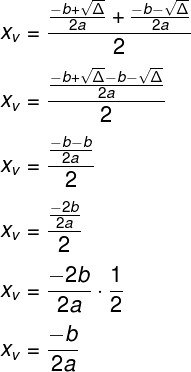
Replacing this value in the occupation f(x) = ax2 + bx + c, we have:

Doing the least common multiple of the denominators, we find:
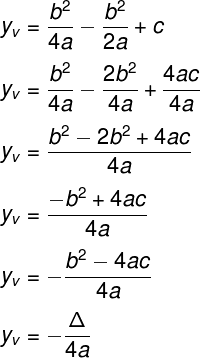
Example
Find the coordinates of the vertex of the occupation f(x) = x2 – 16.
Using the formulas, we get:
xv = - B
2nd
xv = – 0
2
xv = 0
yv = – Δ
4th
yv = - (B2 – 4·a·c)
4th
yv = – (02 – 4·1·(– 16))
4
yv = – (– 4·(– 16))
4
yv = – (64)
4
yv = – 16
At coordinatesofvertex of this function are V (0, – 16).
By Luiz Paulo Moreira
Graduated in Mathematics
Source: Brazil School - https://brasilescola.uol.com.br/matematica/coordenadas-vertice-parabola.htm