An important application of Mathematics in Physics is given by the rate of variation of the 2nd degree function, which is linked to uniformly varied movement, that is, situations in which the speed varies according to the acceleration. The 2nd degree function is given by the expression ax² + bx + c = 0 and its rate of change in an interval (x, x+h), with x and x+h Є R and h ≠ 0, is given by the expression:
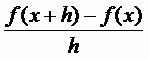
In the case of the 2nd degree function, we have:
f (x+h) = a (x+h) ² + b (x+h) + c = a (x² + 2xh + h²) + bx + bh + c = ax² + 2axh + ah² + bx + bh + c
Then:
f (x+h) - f (x) = ax² + 2axh + ah² + bx + bh + c - (ax² + bx + c) = ax² + 2axh + ah² + bx + bh + c - ax² - bx - c = 2axh + ah² + bh
So we have:
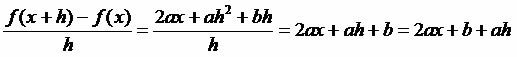
According to the above expression, when h approaches zero, the rate of change will approach 2ax + b. In this way, we can express this situation through a graph, which clearly demonstrates that the rate of variation of the quadratic function, when h approaches zero, is the slope of the tangent line to the parabola. y = ax² + bx + c on point (x0y0).
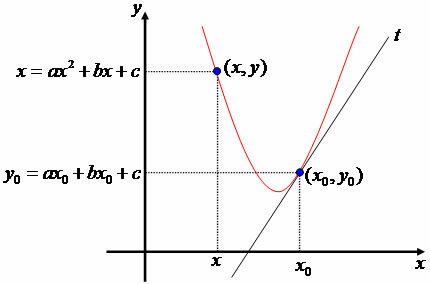
The slope of the tangent line t at the point (x0yy0) is given by 2x0 + b.
Example
A uniformly varied movement is given by the expression f (t) = at² + bt + c, which gives the position of an object at a certain time t. In the expression, a is the acceleration, t is the time, b is the initial velocity, and c is the object's initial position.
For f (t) = at² + bt + c:
f (t+h) = a (t+h) ² + b (t+h) + c = a (t² + 2th + h²) + bt + bh + c = at² + 2ath + ah² + bt + bh + c
f (t+h) - f (t) = at² + 2ath + ah² + bt + bh + c - at² - bt - c = 2ath + ah² + bh

When h approaches zero, the average speed value will approach 2at + b. Therefore, the expression that determines the speed of this object from the expression of space as a function of time is:
v (t) = 2at + b
by Mark Noah
Graduated in Mathematics
Brazil School Team
Roles - Math - Brazil School
Source: Brazil School - https://brasilescola.uol.com.br/matematica/taxa-variacao-funcao-2-grau.htm


