We say that two linear systems are equivalent when they have the same solution set. To perform equivalence between two systems we need to apply the system resolution techniques: addition method or substitution method.
The following two systems are equivalent in that they have the same solution set. Watch:
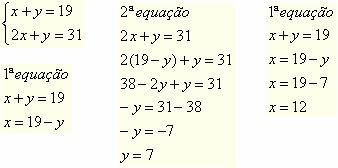

Using the methods shown above, we can create situations in order to perform equivalence between two systems. Look:
Example 1
Determine the values of a and b so that the following systems are equivalent.

Let's solve the system in which the coefficients have given values.

Now let's replace the values of x and y in the system with coefficients a and b.
ax + 3y = 21 → a * 9 + 3 * 1 = 21 → 9a + 3 = 21 → 9a = 21 – 3 → 9a = 18 → a = 2
6x + by = 55 → 6 * 9 + b * 1 = 55 → 54 + b = 55 → b = 55 – 54 → b = 1
The coefficients a and b must assume the values 2 and 1 respectively, so that the systems are equivalent.
Example 2
Determine the value of the coefficient k Є R so that the following systems are equivalent.


Determining the value of the coefficient k.
kx + y = 3k + 5
k * 1 + 1 = 3k + 5
k + 1 = 3k + 5
k – 3k = 5 – 1
–2k = 4
2k = –4
k = -4/2
k = –2
by Mark Noah
Graduated in Mathematics
Brazil School Team
Equation - Math - Brazil School
Source: Brazil School - https://brasilescola.uol.com.br/matematica/equivalencia-entre-sistemas-lineares.htm
