Some situations involving geometric progressions receive special attention regarding development and solution. Certain geometric sequences, when added, tend to a fixed numerical value, that is, the introduction of new terms in the sum makes as the geometric series comes closer and closer to a value, this type of behavior is called a Geometric Series Convergent. Let's analyze the following geometric progression (4, 4/3, 4/9, 4/27, ...) of reason q = 1/3, determining the following situations: Y5 and S10.
Sum of Terms of a Geometric Progression
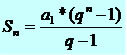

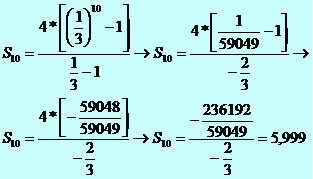
As the number of terms increases, the value of the sum of the terms in the progression approaches 6. We conclude that the sum of the sequence (4, 4/3, 4/9, 4/27, ...) converges to 6 whenever new elements are introduced. We can demonstrate the general situation as follows: 4 + 4/3 + 4/9 + 4/27 +... = 6.
Another situation involving Geometric Progressions is the Divergent Series, which do not tend to a number fixed as the Convergents, as they increase more and more as new terms are introduced to the progression. Watch the PG
(3, 6, 12, 24, 48, ...) of ratio q = 2, let's determine the sums when: n = 10 and n = 15.

Note that the sum increased with the number of terms, S10 = 3069 and S15 = 98301, so we say that the series diverges, it gets as big as you want.
Returning to the study of Convergent Series, we can determine a single expression that expresses the value to which the geometric series approaches, for that we will consider some points. Let's assume that the ratio q assumes values within the range ] – 1 and 1[, that is – 1 < q < 1, thus, we can conclude that the element qn of the expression that determines the sum of terms of a PG tends to zero as the number of terms n increases. In this way, we can consider qn = 0. Follow the demo:
sno = The1(qn – 1) = The1(0 – 1) = – The1 = The1
what – 1 q – 1 q – 1 1 – what
So, the following expression follows:
sno = The1, –1 < q < 1
1 – what
by Mark Noah
Graduated in Mathematics
Brazil School Team
Progressions - Math - Brazil School
Source: Brazil School - https://brasilescola.uol.com.br/matematica/series-geometricas-convergentes-divergentes.htm

