In several situations we can have an electrical circuit made up of resistors connected both in parallel and in series. These circuits are called mixed circuit. Although this type of circuit seems complex to us, we can find the equivalent resistor. For this, we just need to analyze the problem by parts.
Let's look at the figure above. We can see that this is not a simple electrical circuit, in the sense that all resistors are connected in series or in parallel. We can see that resistors 1 and 2 are connected in parallel, whereas resistor 3 is connected in series with the set of resistors 1 and 2.
In order to find the equivalent resistor from the above circuit, first we have to combine resistors 1 and 2 and replace them with the equivalent resistor RP with resistance.
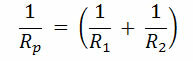
In this way, the new circuit configuration has only two resistors in series (RP and R3), which can now be replaced by just an equivalent resistor R:
R = RP + R3
Using this method we can analyze several mixed electrical circuits, always finding, first, the equivalent resistor for each set of resistors. When the equivalent resistance is found, we can also find the value of the electric current that runs through it and also find the value of ddp and power dissipated by each resistor.
Mind Map: Mixed Circuits
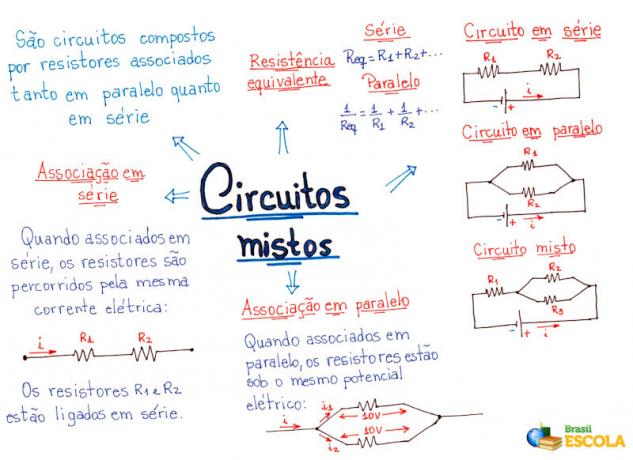
*To download the mind map in PDF, Click here!
Let's see the example below:
What is the value of the electrical current flowing through the following circuit and the total power dissipated in it? The battery provides 25 volts and all resistors are 100 ?.
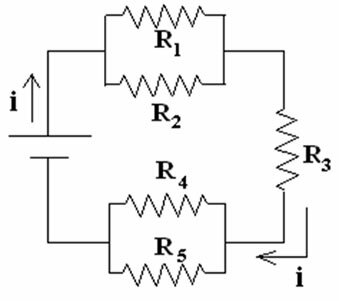
Mixed electrical circuit
Initially we must find the equivalent resistance value for the mixed circuit. The electrical current can be calculated using the following equation: (U = R. i), and power can be determined directly from resistance and current values.
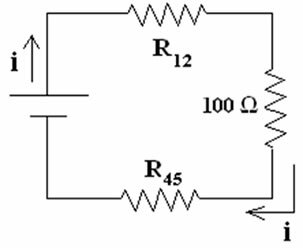
Electrical circuit with resistors associated in series
First, we combine the resistors that are in parallel. the set R1 and R2 can be replaced by an equivalent resistance resistor:
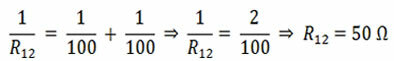
The same is true for the set R4 and R5. We are left with a circuit composed of 3 resistors in series, with resistances of 50, 100 and 50?. The equivalent resistance of this set is:
R = 50 + 100 + 50 = 200 ?
We see that the current passing through the circuit is:
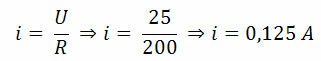
The total dissipated power is:
P = R.i2 ⇒ P=200.(0.125)2 ⇒ P = 3.125 W
By Domitiano Marques
Graduated in Physics
*Mental Map by Me. Rafael Helerbrock
Source: Brazil School - https://brasilescola.uol.com.br/fisica/circuitos-mistos.htm

