O Briot-Ruffini's practical device it's a way to split a polynomial of degree n > 1 by a 1st degree binomial of the form x – a. This method is a simple way to perform the division between a polynomial and a binomial, since to perform this operation using the definition is quite laborious.
Read too: What is a polynomial?
Step by step division of polynomials by the Briot-Ruffini method
This device can be used in the division between a polynomial P(x) that has degree n greater than 1 (n >1) and a binomial of type (x – a). Let's follow the step-by-step example in the following example:
Example
Using the practical Briot-Ruffini device, divide the polynomial P(x) = 3x3 + 2x2 + x +5 by the binomial D(x) = x +1. |
Step 1 – Draw two line segments, one horizontally and one vertically.

Step 2 – Place the coefficients of the polynomial P(x) on the horizontal line segment and to the right of the vertical segment and repeat the first coefficient at the bottom. On the left side of the vertical segment, we must place the root of the binomial. To determine the root of a binomial, just set it to zero, like this:
x + 1 = 0
x = – 1
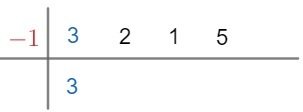
Step 3 – Let's multiply the root of the divisor by the first coefficient located below the horizontal line and then add the result by the next coefficient located above the horizontal line. Then, let's repeat the process until the last coefficient, in this case coefficient 5. Look:

After performing these three steps, let's look at what the algorithm gives us. At the top of the horizontal line and to the right of the vertical line, we have the coefficients of the polynomial P(x), like this:
P(x) = 3x3 + 2x2 + x +5
The number –1 is the root of the divisor and therefore the divisor is D(x) = x + 1. Finally, the quotient can be found with the numbers located below the horizontal line, the last number being the rest of Division.
remember that the dividend grade is 3 it's the divider degree is 1, so the degree of the quotient is given by 3 – 1 = 2. So, the quotient is:
Q(x) = 3x2 – 1x + 2
Q(x) = 3x2 – x + 2
Note again that the coefficients (marked in green) are obtained with the numbers below the horizontal line and that the remainder of the division is: R(x) = 3.
Using the division algorithm, We have to:
Dividend = Divisor · Quotient + Rest
3x3 + 2x2 + x +5 = (x + 1) · (3x2 – x + 2) + 3

solved exercises
question 1 – (Furg) In the division of a polynomial P(x) by the binomial (x – a), when using the practical Briot-Ruffini device, we found:
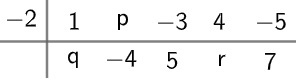
The values of a, q, p and r are, respectively:
a) – 2; 1; – 6 and 6.
b) – 2; 1; – 2 and – 6.
c) 2; – 2; – 2 and – 6.
d) 2; – 2; 1 and 6.
e) 2; 1; – 4 and 4.
Solution:
Note that the statement states that the polynomial P(x) was divided by the binomial (x – a), so it will be the divisor. From the practical Briot-Ruffini device, we have that the number to the left of the vertical line is the root of the divisor, so a = – 2.
Also based on the practical Briot-Ruffini device, we know that it is necessary to repeat the first coefficient of the dividend below the horizontal line, therefore q = 1.
To determine the value of p, let's use the handy device again. Look:

– 2 · q + p = – 4
We know that q = 1, discovered earlier, like this:
– 2 · 1 + p = – 4
– 2 + p = – 4
p = – 4 + 2
p = –2
Similarly, we have to:
– 2 · 5 +4 = r
– 10 + 4 = r
r = – 6
Therefore, a = – 2; q = 1; p = –2; r = – 6.
Answer: alternative b.
Read too: Division of polynomials - tips, methods, exercises
Question 2 - Divide the polynomial P(x) = x4 – 1 by the binomial D(x) = x – 1.
Solution:
Note that the polynomial P(x) is not written in its complete form. Before applying the practical Briot-Ruffini device, we must write it in its complete form. Look:
P(x) = x4 + 0x3 + 0x2 + 0x – 1
Having made this observation, we can continue Briot-Ruffini's practical device. Let's determine the root of the divisor and then apply the algorithm:
x - 1 = 0
x = 1

We can conclude that by dividing the polynomial P(x) = x4 – 1 by the binomial D(x) = x – 1, we have the following: polynomial Q(x) = x3 + x2 + x + 1 and remainder R(x) = 0.
by Robson Luiz
Maths teacher
Source: Brazil School - https://brasilescola.uol.com.br/matematica/divisao-polinomios-utilizando-dispositivo-briotruffini.htm