A tangent (abbreviated as tg or tan) is a trigonometric function. To determine the tangent of an angle, we can use different strategies: calculate the ratio between the sine and cosine of the angle, if they are known; use a tangent table or a calculator; calculate the ratio between the opposite leg and the adjacent one, if the angle in question is internal (acute) of a right triangle, among others.
Read too: What is the trigonometric circle used for?
summary about tangent
Tangent is a trigonometric function.
The tangent of an interior angle to a right triangle is the ratio of the opposite side to the adjacent side.
The tangent of any angle is the ratio of the sine and cosine of that angle.
The function \(f (x)=tg\ x\) is defined for angles x expressed in radians, such that cos \(cos\ x≠0\).
The graph of the tangent function shows vertical asymptotes for the values, where \(x= \frac{π}2+kπ\), with k whole, like \(x=-\frac{π}2\).
The law of tangents is an expression that associates, in any triangle, the tangents of two angles and the sides opposite those angles.
Tangent of an angle
If α is one angle internal of a right triangle, the tangent of α is the ratio between the length of the opposite leg and the length of the adjacent leg:
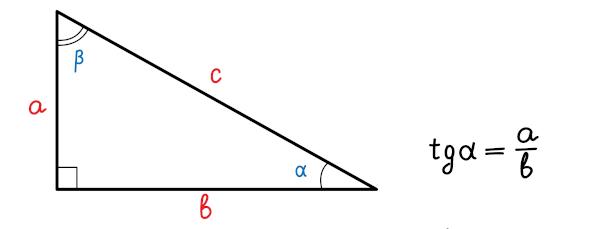
For any angle α, the tangent is the ratio between the sin α and the cosine of α, where \(cos\ α≠0\):
\(tg\ α=\frac{sin\ α}{cos\ α}\)
It should be noted that if α is an angle in the 1st or 3rd quadrant, the tangent will have a positive sign; but if α is an angle of the 2nd or 4th quadrant, the tangent will have a negative sign. This relationship results directly from the sign rule between the signs of sine and cosine for each α.
Important: Note that the tangent does not exist for values of α where \(cos\ α=0\). This happens for angles of 90°, 270°, 450°, 630° and so on. To represent these angles in a general way, we use radian notation: \(\frac{ π}2+kπ\), with k whole.
Tangent of notable angles
Using the expression \(tg\ α=\frac{sin\ α}{cos\ α}\), we can find the tangents of remarkable angles, which are the angles of 30°, 45° and 60°:
\(tg\ 30°=\frac{sin\ 30°}{cos\ 30°}=\frac{\frac{1}{2}}{\frac{\sqrt3}{2}}=\frac{1}{\sqrt3}=\frac{\sqrt3}{3}\)
\(tg\ 45°=\frac{sin\ 45°}{cos\ 45°} = \frac{\frac{\sqrt2}{2}}{\frac{\sqrt2}{2}}=1\)
\(tg\ 60°=\frac{sin\ 60°}{cos\ 60°}=\frac{\frac{\sqrt3}{2}}{\frac{1}2}=\sqrt3\)
Interesting: In addition to these, we can analyze the tangent values for the angles of 0° and 90°, which are also widely used. Since sin 0° = 0, we conclude that tan 0° = 0. For the 90° angle, since cos90° = 0, the tangent does not exist.
How to calculate the tangent?
To calculate the tangent, we use the formula tg α=sin αcos α, used for calculating the tangent of any angle. Let's look at some examples below.
Example 1
Find the tangent of angle α in the right triangle below.
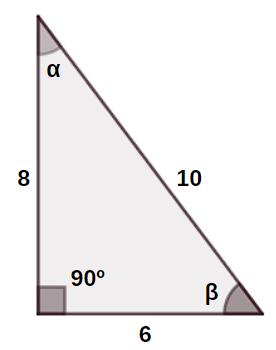
Resolution:
Regarding the angle α, the side of measure 6 is the opposite side and the side of measure 8 is the adjacent side. Like this:
\(tg\ α=\frac{6}8=0.75\)
Example 2
Knowing that \(sin\ 35°≈0.573\) and cos\(35°≈0,819\), find the approximate value for the 35° tangent.
Resolution:
Since the tangent of an angle is the ratio between the sine and cosine of that angle, we have:
\(tg\ 35°=\frac{sin\ 35°}{cos\ 35°}= \frac{0.573}{0.819}\)
\(tg\ 35°≈0.700\)
tangent function
The function fx=tg x is defined for angles x expressed in radians, so that \(cos\ x≠0\). This means that the domain of the tangent function is expressed by:
\(D(tg)=\{x∈ \mathbb{R}:x≠\frac{π}2+kπ, k∈ \mathbb{Z} \}\)
Furthermore, all real numbers are the image of the tangent function.
→ Graph of the tangent function

Note that the graph of the tangent function has vertical asymptotes for the values where \(x= \frac{π}2+kπ\), with k whole, like \( x=-\frac{π}2\). For these values of x, the tangent is not defined (that is, the tangent does not exist).
See too: What is domain, range and image?
law of tangents
The law of tangents is a expression that associates, in a triangle any, the tangents of two angles and the sides opposite those angles. For example, consider angles α and β of triangle ABC below. Note that the side CB = a is opposite the angle α and that the side AC = b is opposite the angle β.
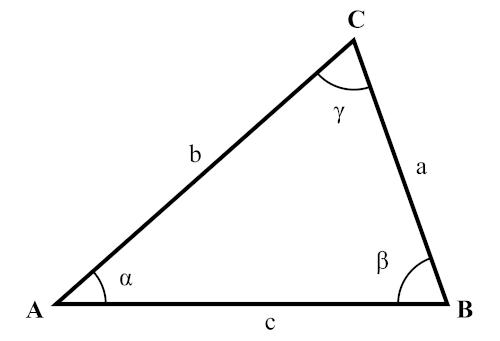
The law of tangents states that:
\(\frac{a-b}{a+b}=\frac{tg\ [\frac{1}2(α-β)]}{tg\ [\frac{1}2 (α+β)]}\)
trigonometric ratios
To the trigonometric ratios are the trigonometric functions worked on the right triangle. We interpret these ratios as relationships between the sides and angles of this type of triangle.

Solved exercises on tangent
question 1
Let θ be an angle of the second quadrant such that sin\(sin\ θ≈0.978\), so tgθ is approximately:
A) -4,688
B) 4,688
C) 0.2086
D) -0.2086
E) 1
Resolution
Alternative A
if \(sin\ θ≈0.978\), then, using the fundamental identity of trigonometry:
\(sin^2 θ+cos^2 θ=1\)
\(0.978^2+cos^2 θ=1\)
\(cos^2 θ=1-0.956484\)
\(cos\ θ=±\sqrt{0.043516}\)
Since θ is an angle of the second quadrant, then cosθ is negative, therefore:
\(cos\ θ≈- 0.2086\)
Soon:
\(tg\ θ=\frac{sin\ θ}{cos\ θ}=\frac{0.978}{-0.2086}=-4.688\)
question 2
Consider a right triangle ABC with legs AB = 3 cm and AC = 4 cm. The tangent of angle B is:
A) \(\frac{3}4\)
B) \(\frac{3}5\)
W) \(\frac{4}3\)
D) \(\frac{4}5\)
AND) \(\frac{5}3\)
Resolution:
Alternative C
By the statement, the leg opposite the angle \(\hat{B}\) is the AC measuring 4 cm and the leg adjacent to the angle \(\hat{B}\) is AB with a measure of 3 cm. Like this:
\(tg\hat{C}=\frac{4}3\)
By Maria Luiza Alves Rizzo
Math teacher


