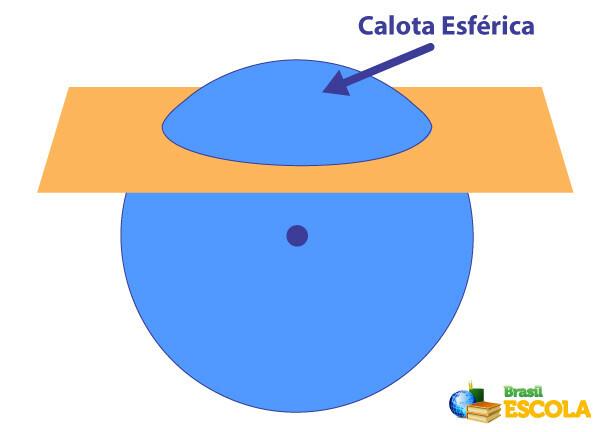
A spherical cap and the geometric solid obtained when a sphere is intercepted by a plane, dividing it into two geometric solids. The spherical cap is considered a round body because, like the sphere, it has a rounded shape. To calculate the area and volume of a spherical cap, we use specific formulas.
Read too: Trunk of cone — the geometric solid formed by the bottom of the cone when a section parallel to the base is made
Topics of this article
- 1 - Summary on spherical cap
- 2 - What is a spherical cap?
- 3 - Elements of the spherical cap
- 4 - Is the spherical cap a polyhedron or a round body?
- 5 - How to calculate the radius of the spherical cap?
- 6 - How to calculate the area of the spherical cap?
- 7 - How to calculate the volume of the spherical cap?
- 8 - Solved exercises on spherical cap
Summary about spherical cap
- The spherical cap is a geometric solid obtained when the sphere is divided by a plane.
- The main elements of the spherical cap are the radius of the sphere, the radius of the spherical cap and the height of the spherical cap.
- The spherical cap is not a polyhedron, but a round body.
- If the plane divides the sphere in half, the spherical cap forms a hemisphere.
- It is possible to calculate the radius of the spherical cap using the Pythagorean theorem, organized as follows:
\(\left (R-h\right)^2+r^2=R^2\)
- The area of the spherical cap can be calculated using the formula:
\(A=2\pi rh\ \)
- The volume of the spherical cap can be calculated using the following formula:
\(V=\frac{\pi h^2}{3}\cdot\left (3r-h\right)\)
Do not stop now... There's more after the publicity ;)
What is a spherical cap?
spherical cap is the geometric solid obtained when a section of the ball common flat. When we cut the sphere with a plane, we divide this sphere into two spherical caps. When we divide the sphere in half, the spherical cap is known as the hemisphere.
Spherical cap elements
In a spherical cap, the main elements are the radius of the sphere, the radius of the spherical cap and the height of the spherical cap.
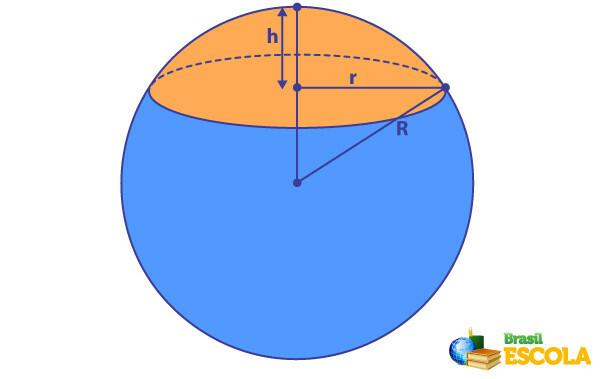
- R → radius of the sphere.
- r → radius of the spherical cap.
- h → height of the spherical cap.
Is the spherical cap a polyhedron or a round body?
We can see that the cap is a geometric solid. As it has a circular base and a rounded surface, the spherical cap is considered a round body, which is also known as the solid of revolution. It is worth mentioning that the polyhedron has faces formed by polygons, which is not the case of the spherical cap, which has a base formed by a circle.
How to calculate the radius of the spherical cap?
To calculate the radius length of the spherical cap, it is necessary to know the length of the height h of the spherical cap and the length of the radius R of the sphere, because, as we can see in the following image, there is a Pythagorean relationship.
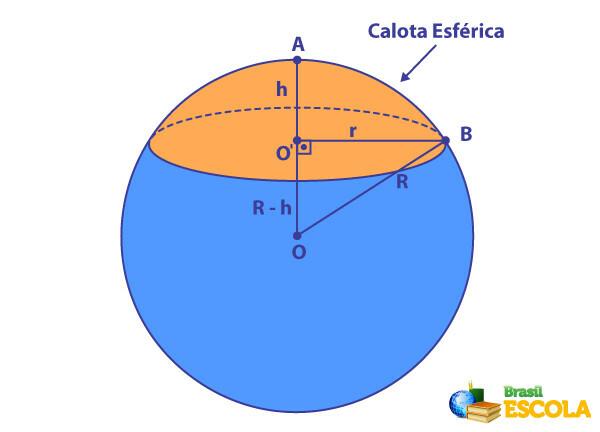
Note that we have a right triangle, the triangle OO’B, with hypotenuse measuring R and legs measuring R – h and r. Applying the Pythagorean theorem, We have to:
\(\left (R-h\right)^2+r^2=R^2\)
Example:
What is the radius of a spherical cap that has a height of 2 cm, given that the radius of the sphere is 5 cm?
Resolution:
Applying the Pythagorean relation:
\(\left (R-h\right)^2+r^2=R^2\)
\(\left (5-2\right)^2+r^2=5^2\)
\(3^2+r^2=25\)
\(9+r^2=25\)
\(r^2=25-9\)
\(r^2=16\)
\(r=\sqrt{16}\)
\(r=4\)
How to calculate the area of the spherical cap?
To calculate the area of the spherical cap, it is necessary to know the measurement of the length of the radius R of the sphere and the height h of the cap. The formula used to calculate the surface area is:
\(A=2\pi Rh\)
- R → radius of the sphere.
- h → height of the spherical cap.
Example:
A spherical cap was obtained from a sphere that has a radius of 6 cm and a height of 4 cm. So what is the surface area of this spherical cap?
Resolution:
Calculating the area of the spherical cap, we have:
\(A=2\pi Rh\)
\(A=2\cdot\pi\cdot6\cdot4\ \)
\(A=48\pi\ cm^2\)
How to calculate the volume of the spherical cap?
The volume of the spherical cap can be calculated in two ways. The first formula depends on the radius R of the sphere and the height h:
\(V=\frac{\pi h^2}{3}\left (3 R-h\right)\)
Example:
What is the volume of a spherical cap obtained from a sphere of radius 8 cm whose height of the spherical cap is 6 cm?
Resolution:
Since we know the value of R and h, we will use the first formula.
R = 8
h = 6
\(V=\frac{\pi h^2}{3}\left (3 R-h\right)\)
\(V=\frac{\pi6^2}{3}\left (3\cdot8-6\right)\)
\(V=\frac{36\pi}{3}\left (24-6\right)\)
\(V=12\pi\left (18\right)\)
\(V=216\pi\ cm^3\)
The other spherical cap volume formula takes into account the spherical cap radius r and the cap height h:
\(V=\frac{\pi h}{6}\left (3r^2+h^2\right)\)
Example:
What is the volume of a spherical cap that has a radius of 10 cm and a height of 4 cm?
Resolution:
In this case, we have r = 10 cm and h = 4 cm. As we know the value of the radius of the spherical cap and the height, we will use the second formula:
\(V=\frac{\pi h}{6}\left (3r^2+h^2\right)\)
\(V=\frac{4\pi}{6}\left (3{\cdot10}^2+4^2\right)\)
\(V=\frac{4\pi}{6}\left (3\cdot100+16\right)\)
\(V=\frac{4\pi}{6}\left (300+16\right)\)
\(V=\frac{4\pi}{6}\left (316\right)\)
\(V=\frac{1264\pi}{6}\)
\(V\approx210.7\ \pi\ cm³\)
See too: Pyramid trunk — the geometric solid formed by the bottom of the pyramid when a cross section is taken
Solved exercises on spherical cap
question 1
(Enem) To decorate a children's party table, a chef will use a spherical melon with a diameter measuring 10 cm, which will serve as a support to skewer various sweets. He will remove a spherical cap from the melon, as shown in the figure, and, to guarantee the stability of this support, making it difficult for the melon to roll across the table, the chef will cut so that the radius r of the circular cut section is at least minus 3 cm. On the other hand, the boss will want to have as much area as possible in the region where the sweets will be posted.

In order to achieve all his objectives, the chef must cut the top of the melon at a height h, in centimeters, equal to
A) \(5-\frac{\sqrt{91}}{2}\)
B)\( 10-\sqrt{91}\)
C) 1
D) 4
E) 5
Resolution:
Alternative C
We know that the diameter of the sphere is 10 cm, so its radius is 5 cm, so OB = 5 cm.
If the radius of the section is exactly 3 cm, we have:
AO² +AB² = OB²
AO² + 3² = 5²
AO² + 9 = 25
AO² = 25 – 9
AO² = 16
AO = \(\sqrt{16}\)
AO = 4 cm
Therefore:
h + 4 = 5
h = 5 – 4
h = 1
question 2
A spherical cap has an area of 144π cm². Knowing that it has a radius of 9 cm, the height of this spherical cap is:
A) 8 cm
B) 10 cm
C) 14 cm
D) 16 cm
E) 22 cm
Resolution:
Alternative A
We know that:
\(A=2\pi Rh\)
\(144\pi=2\pi\cdot9\cdot h\)
\(144\pi=18\pi h\)
\(\frac{144\pi}{18\pi}=h\)
\(8=h\)
The height is 8 cm.
By Raul Rodrigues de Oliveira
Maths teacher
Would you like to reference this text in a school or academic work? Look:
OLIVEIRA, Raul Rodrigues de. "Spherical cap"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/calota-esferica.htm. Accessed on July 20, 2023.
Click here and learn all about the cylinder, a geometric solid that is very present in our daily lives. Learn their formulas and learn how to use each one of them!
Learn what a cone is, how to calculate its total area and volume, as well as its main classifications and identify the flatness of this solid.
Click here and find out what round bodies are. Know its characteristics and formulas. Learn the difference between a round body and a polyhedron.
Click to better understand the elements of a sphere and also learn how to perform calculations involving these elements!
Know what a sphere is and what are the elements that constitute it. Learn to calculate the volume and total area of this geometric solid and solve the exercises.
Find out how to calculate the volume of the sphere. Read about this geometric solid and its formulas.
Cringe
The slang adapted from English is used to designate someone who is seen as tacky, shameful, outdated and out of fashion.
Neurodiversity
A term coined by Judy Singer, it is used to describe the wide variety of ways the human mind behaves.
PL of Fake News
Also known as PL2660, it is a bill that establishes mechanisms for the regulation of social networks in Brazil.