To the basic operations in mathematics are the most elementary processes carried out between numbers: the addition, subtraction, multiplication and division. Each of these operations has properties that can be exploited to facilitate calculations.
An important observation when solving mathematical operations is to identify in which set the worked elements are. Consider that, throughout this text, all numbers are real. For the study of integers, read the specific articles for each basic operation indicated at the end of the page.
Read too: What are number sets?
Topics of this article
- 1 - Summary of basic mathematical operations
-
2 - What are the basic mathematical operations?
- ? Addition
- ? Subtraction
- ? Multiplication
- ? Division
- 3 - Solved exercises on basic mathematical operations
Summary of basic math operations
Addition, subtraction, multiplication and division are the basic mathematical operations.
Subtraction is the reverse operation of addition, and division is the reverse operation of multiplication.
The result of an addition is the sum, and the result of a subtraction is the difference.
The result of a multiplication is the product, and the result of a division is the quotient.
What are the basic math operations?
The basic mathematical operations are addition, subtraction, multiplication and division. Two relationships between these operations should be highlighted:
Subtraction is the reverse operation of addition.
Division is the inverse operation of multiplication.
Let's get to know a little more about each one and, at the end of the text, solve some problems associated with basic operations.
➝ Addition
The addition operation involves adding, adding, joining. this operation is indicated by the symbol + and has the following structure:
\(a+b=c\)
on what w and the sum of installmentsThe It is B. We read “a plus b equals c”. Remembering that The, B It is w represent real numbers.
Examples:
\(1+2=3\)
\(24+30=54\)
\(-1+7=6\)
\(1,25+2=2,25\)
\(x+x=2x\)
Observation: A number line is an important tool for the study of addition.
properties of addition
commutativity: if The It is B are real numbers, so \(a+b=b+a \).
That is, the order of the parcels does not change the sum. Note that, for example, \(3+10=13\ and\ 10+3=13 \).
Associativity: if The, B It is w are real numbers, so \(a+(b+c)=(a+b)+c \).
Note that, for example, \(2+(1+3)=2+4=6 \) It is \((2+1)+3=3+3=6 \).
Elementneutral: element 0 is neutral for the addition operation. that is, if The is a real number, then a+0=a .
Note that, for example, \(7+0=7 \).
Elementopposite (or symmetrical): if The is a real number, then \(-The \) is called the opposite element to The It is \(a+(-a)=0 \).
Note that, for example, \(5+(-5)=0\).
Observation: To understand the last property and solve different problems related to the four basic operations, it is fundamental to know the rule of signs.
➝ Subtraction
The subtraction operation involves subtracting, subtracting, removing. this operation is indicated by the symbol \(\mathbf{-}\) and has the following structure:
\(a-b=c\)
on what w and the difference in between The It is B. We read "a minus b equals c".
Examples:
\(6-1=5\)
\(32-11=21\)
\(- 4-3=-7\)
\(10,5-4,75=5,75\)
\(8z-z=7z\)
Observation: The number line can also be used to study subtraction.
➝ Multiplication
The multiplication operation involves multiplying, adding up. this operation is indicated by different symbols such as \(×\), \(*\)It is \(\cdot\) and has the following structure:
\(a×b=c\)
on what w and the product between the factorsThe It is B. We read “a times b equals c”.
Examples:
\(2 ×3 =6\)
\(4×(-2)=-8\)
\(x*x=x^2\)
multiplication properties
commutativity: if The It is B are real numbers, so \(a×b=b×a\).
That is, the order of the factors does not change the product. Note that, for example, \(- 9×2=- 18\) It is \(2×- 9 =- 18\).
Distributiveness: if The, B It is w are real numbers, so \(a×(b+c)=a×b+a×c\).
Note that, for example, \(3×(9+4)=3×13=39\) It is \(3×9+3×4=27+12=39\).
This property (known as “chuveirinho”) is also valid in relation to subtraction, that is, \(a×(b-c)=a×b-a×c\).
Associativity: if The, B It is w are real numbers, so \(a×(b×c)=(a×b)×c\).
Note that, for example, \(10×(5×8)=10×40=400\) It is \((10×5)×8=50×8=400\).
Elementneutral: element 1 is neutral for the multiplication operation. that is, if The is a real number, then \(a×1=a\).
Note that, for example, \(2×1=2\).
Elementreverse: if The is a real number, then \(\frac{1}a\) is called the multiplicative inverse of The It is \(a×\frac{1}a=1\).
For example, \(6×\frac{1}6=1\).
➝ Division
The division operation involves dividing, fragmenting, segmenting. this operation is indicated by the symbol \(÷\) and has the following structure:
\(a÷b=c\)
on what B is different from zero and w is the quotient or ratio of The It is B. We read “a divided by b equals c”.
A division can be exact when the result is an integer or non-exact when the result is not an integer.
It is important to note that if \(a÷b=c \), then \(b×c=a \).
Examples:
\(27÷9=3\)
\(20÷8=2,5\)
\(3,2÷1,6=2\)
\(12x÷4=3x\)
Read too: How to solve operations with fractions?
Solved exercises on basic mathematical operations
question 1
(Enem 2022) A higher education institution offered vacancies in a selection process for access to its courses. After registration was completed, the list of the number of candidates per vacancy in each of the courses offered was released. These data are presented in the table.
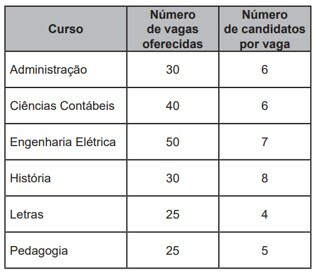
What was the total number of candidates enrolled in this selection process?
a) 200
b) 400
c) 1200
d) 1235
e) 7200
Resolution
Alternative D
The total number of candidates enrolled in the selection process is given by the sum of the number of candidates enrolled for each course. And this information is obtained by the product between the number of vacancies offered and the number of candidates per vacancy.
Administration: \(30×6=180 \) enrolled candidates.
Accounting Sciences: \(40×6=240 \) enrolled candidates.
Electrical engineering: \(50×7=350 \) enrolled candidates.
History: \(30×8=240 \) enrolled candidates.
Letters: \(25×4=100 \) enrolled candidates.
Pedagogy: \(25×5=125 \) enrolled candidates.
Therefore, the number of candidates enrolled in the selection process was \(180+240+350+240+100+125=1235\).
Do not stop now... There's more after the publicity ;)
question 2
(Enem 2016 — adapted) The table shows the ranking order of the first six countries in a day of dispute at the Olympics. Sorting is done according to the amount of gold, silver and bronze medals, respectively.

Which country won 3 more medals than France and Argentina combined?
the China.
b) USA
c) Italy
d) Brazil
Resolution
Alternative A
Note that, together, France and Argentina won 14 medals \((7+7=14 )\).
Note that:
China won 17 medals, i.e. 3 more medals than France and Argentina combined \((17-14=3 )\).
USA won 16 medals, i.e. 2 more medals than France and Argentina combined \((16-14=2 )\).
Italy won 10 medals, i.e. 4 medals less than France and Argentina combined \((10-14=-4 )\).
Brazil won 10 medals, that is, 4 medals less than France and Argentina together \((10-14=-4 )\).
By Maria Luiza Alves Rizzo
Math teacher
Would you like to reference this text in a school or academic work? Look:
RIZZO, Maria Luiza Alves. "Basic Mathematical Operations"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/operacoes-matematicas-basicas.htm. Accessed on July 18, 2023.
Learn the addition of integers greater than zero and learn the properties of this basic mathematical operation.
Learn the main numerical sets and their main characteristics. Also find out how real intervals are classified.
Know the division algorithm. Find out who your constituents are. Follow the examples and the solved exercise in order to better understand this calculation.
Learn to use the sign game to find the sign of the result of a multiplication or addition and expand this concept to other operations.
Click and learn what a number line is, learn how to build it and how the one-to-one relationship between it and real numbers is established.
Click to learn how to perform a subtraction and learn some tips about this basic mathematical operation.


