Two quantities are known as directly proportional when they relate proportionally and directly. This means that, in a situation involving these quantities, if one of them increasesr its value, the other will also increase in the same proportion, that is, if one magnitude doubles its value, the other will also double its value.
In our daily lives, there are several situations in which it is possible to identify magnitudes that are directly proportional, such as the relationship between the weight of a given product and the amount to be paid for it, or the relation between labor time and the production of a given machine.
The fact that the magnitudes are directly proportional makes it possible predict the behavior of these quantities through of the proportionality ratio. In addition to directly proportional quantities, there are also inversely proportional quantities, which are those that are inversely related, such as velocity and time at a given route.
Read too: 3 Most Common Mistakes When Using the Rule of Three
Topics of this article
- 1 - Summary of directly proportional quantities
- 2 - What are directly proportional quantities?
- 3 - How to calculate directly proportional quantities?
- 4 - Difference between directly proportional and inversely proportional quantities
- 5 - Video lesson on proportional quantities in Enem
- 6 - Solved exercises on directly proportional quantities
Summary on directly proportional quantities
Two quantities are directly proportional when they increase or decrease by the same amount.
You can use this proportionality to calculate unknown values.
There are several situations in our daily lives with directly proportional magnitudes, such as the ratio between the weight of a certain product and the amount to be paid for it.
Do not stop now... There's more after the publicity ;)
What are directly proportional quantities?
We know as greatness everything that can be measured, such as:
time,
speed,
distance,
density,
strength,
pasta,
among many other examples in our daily lives.
There are situations in our daily lives in which there is more than one related quantity and it is quite common to compare these quantities to better understand their behavior.
There are specific cases in which these quantities are directly proportional to each other, which means that they increase or decrease in the same proportion. For example, the number of machines and the production of a factory are directly proportional quantities, because if we double the number of machines, the production will also double, and if the number of machines drops by half, the production will also be the same. half. See other examples:
Weight and amount paid for the meat
Distance traveled by a car and fuel consumed
Salary and income tax
Number of guests and amount of food
Read too: percentage — the ratio of any number to 100
How to calculate directly proportional quantities?
When two quantities are directly proportional, it is possible to predict the behavior of one of the quantities for certain situations using the fundamental property of proportions, as we will do in the following example.
Example 1:
In a factory, there are 5 machines that produce 4920 parts daily. On a given day, 2 machines were stopped for maintenance. Knowing that there is no difference in the number of parts produced between the machines, the number of parts produced on that day was?
Resolution:
First, it is possible to notice that these magnitudes are directly proportional, because if I decrease the amount of machines, the amount of parts will decrease in the same proportion, since each machine produces the same amount of parts daily.
Knowing that 5 machines produce 4920 pieces, we want to find how many pieces will be produced by the remaining 3 machines during maintenance. Since the quantities are proportional, the ratio between 5 and 4920 has to be equal to the ratio between 3 and x:
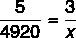
Cross multiplying, we have:
5x = 4920 · 3
5x = 14,760
x = 14,760: 5
x = 2952
This means that 3 machines produce a total of 2,952 parts.
Example 2:
In a butcher shop, a customer orders R$18.00 of a certain type of meat. Knowing that 1 kg of this meat costs R$ 25.00, then how much meat will this customer take?
Resolution:
It is easy to see that these are directly proportional quantities, because if I double the amount of meat, the price will be double, or if I buy half a kilo, the amount paid will also be half the amount paid for 1 kg.
Then, we can set up the proportion, in which x is the weight of R$ 18.00 of this particular type of meat:
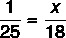
Cross multiplying, we have:
25x = 18 · 1
25x = 18
x = 18: 25
x = 0.72
This means that, with R$ 18 reais, the customer will buy 0.72 kg, which is equal to 720 grams of meat.
Difference between directly proportional and inversely proportional quantities
In addition to directly proportional quantities, there are quantities that can be inversely related. In a given situation involving two quantities, they are classified as inversely proportional when, as we increase the value of one of these quantities, the value of the other quantity decreases accordingly. proportion, such as speed and time to travel a certain route. If we increase the speed, the time that will be spent to make that particular route will be less. To learn more about this other type of relationship between quantities, read the text: Ginversely proportional randencies.
Video lesson on proportional quantities in Enem
Solved exercises on directly proportional quantities
Question 1 - (And either)
alternative sources
There is a new push to produce fuel from animal fat. In April, High Plains Bioenergy opened a biorefinery next to a pork processing plant in Guymon, Oklahoma. The refinery converts the pork fat, along with the vegetable oil, into biodiesel. The factory expects to transform 14 million kilograms of lard into 112 million liters of biodiesel.
Scientific American Magazine. Brazil, Aug. 2009 (adapted).
Consider that there is a direct proportion between the mass of processed lard and the volume of biodiesel produced.
To produce 48 million liters of biodiesel, the mass of lard needed, in kilograms, will be approximately:
A) 6 million.
B) 33 million.
C) 78 million.
D) 146 million.
E) 384 million.
Resolution
Alternative A.
Note that 14 million kilograms of lard are converted into 112 million liters of biodiesel. Let x be the amount of lard needed to produce 48 million liters of biodiesel, we have:
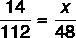
Cross multiplying, we have:
112x = 14 · 48
112x = 672
x=672: 112
x = 6 million
Question 2 - At a direct mail distribution company, João, Marcelo and Pedro are responsible for bagging and labeling magazines.
Once, they received a batch of 6120 magazines and, when they finished the task, they realized that the batch of magazines had been divided into parts directly proportional to the respective working time of each of them in the company.
Knowing that João has been working at the company for 9 months, Marcelo for 12 months and Pedro for 15 months, the number of magazines that João bagged and labeled was:
A) 1 360.
B) 1530.
C) 1890.
D) 2040.
E) 2550.
Resolution
Alternative D.
First we will perform sum two terms: 9 + 12 + 15 = 36. We know that 6120 magazines were dividedto the proportionally to 36 months and that João worked 12 months. Soon, the reason between 36 and 6120 is equal to the ratio between 12 and the x number of magazines that João bagged and labeled:
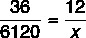
Cross multiplying, we have:
36x = 12 · 6120
36x = 73440
x = 73440: 36
x = 2040
By Raul Rodrigues de Oliveira
Maths teacher
Learn here how to determine if two quantities or numbers are inversely proportional. Check out examples and exercise on the topic!
Learn here what a proportion is and how to calculate it. See also its main properties and understand what proportional quantities are.
Understand what the golden ratio is and see its applications. Learn how to calculate the golden number and what is its relationship with the famous Fibonacci sequence.
See here the different ways to represent a ratio, see also the definition and some applications of proportion. Learn how to apply these concepts.
Learn to use the compound rule of three to find unknown values and problems with three or four quantities.
Know the rule of three. Understand what direct and inversely proportional quantities are. Know the difference between the simple rule of three and the compound rule.