regular polygon and the convex polygon which has all sides congruent and all interior angles congruent, that is, the sides have the same measure and the interior angles also have the same measure. The equilateral triangle and the square are some of the known regular polygons.
Read too: What are the elements of a polygon?
Topics of this article
- 1 - Summary about regular polygon
- 2 - Video lesson on regular polygons
- 3 - What are regular polygons?
- 4 - Perimeter of the regular polygon
- 5 - Internal angles of a regular polygon
- 6 - Exterior angles of a regular polygon
- 7 - Apothem of the regular polygon
- 8 - Area of the regular polygon
- 9 - Difference between regular polygon and irregular polygon
- 10 - Exercises on regular polygons
Summary about regular polygon
Polygon Regular is one that has congruent sides and angles.
The perimeter of a regular polygon is the side length times the number of sides:
\(P = n ⋅l \)
The measure of each interior angle of the regular polygon is given by the following formula:
\(α=\frac{S_i}n\)
The measure of the exterior angle of a regular polygon is given by the following formula:
\(e=\frac{360}n\)
The apothem of a regular polygon is equal to the measure of the radius of a circumscribed circle.
The area of a regular polygon is given by the following formula:
\(A=a⋅p\)
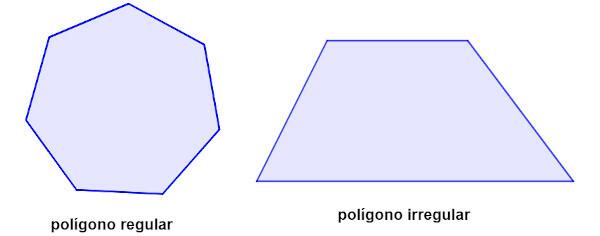
While the regular polygon has all its sides and angles congruent, the irregular polygon does not have all the sides congruent or does not have all the angles congruent.
Video lesson on regular polygons
What are regular polygons?
Regular polygons are convex polygons that are equilateral and equiangular, that is, they have congruent sides and also have angles with the same measure. Remember that polygons are convex when any line segment that has endpoints inside is completely contained within the polygon. O equilateral triangle and the square are cases of regular polygons, but there are pentagons, hexagons, among other polygons that are also regular.
Perimeter of regular polygon
To calculate the perimeter of a regular polygon, just multiply the measure of its side by the number of sides that this polygon has. Since it is equilateral, the perimeter of the regular polygon is calculated by the formula:
\(P=n⋅l\)
n → number of sides of the polygon
l → length of the polygon side
Example:
What is the perimeter of a regular pentagon that has sides measuring 8 cm?
Resolution:
Calculating the perimeter, knowing that the pentagon is regular, we have:
\(P=5⋅8=40\ cm\)
Do not stop now... There's more after the publicity ;)
Interior angles of a regular polygon
A regular polygon is equiangular, that is, all interior angles have the same measure. Therefore, to calculate the value of each angle we can use the sum of the interior angles formula and divide by the number of sides of the polygon.
In general, to calculate the value of the sum of the interior angles of a polygon, we use the formula:
\(S_i=180⋅(n-2)\)
\(S_i\) → sum of the interior angles of the polygon
n → number of sides of the polygon
We know that in a regular polygon all angles are congruent. Therefore, the formula to calculate the measure of each of the angles of a regular polygon is:
\(a_i=\frac{180⋅(n-2)}{n}\)
\(there\) → measure of the interior angle of the polygon
Example:
What is the length of each side of a regular octagon?
Resolution:
replacing n = 8 in the formula, we have:
\(a_i=\frac{180⋅(8-2)}{8}\)
\(a_i=\frac{180⋅6}{8}\)
\(a_i=\frac{1080}8\)
\(a_i=135°\)
Exterior angles of a regular polygon
The sum of the exterior angles of any polygon is 360°. To calculate the measure of each exterior angle of a regular polygon, just divide 360° by the number of sides of this polygon.
\(a_e=\frac{360}n\)
Example:
What is the measure of the exterior angle of an equilateral triangle?
Resolution:
replacing n = 5 in the formula:
\(a_e=\frac{360}3\)
\(a_e=120°\)
Apothem of regular polygon
The apothem of a regular polygon is equal to the measure of the radius of a circumference circumscribed, where the apothem is the length of the segment that goes from the center of the polygon to the side, forming an angle of 90°.

Regular polygon area
To calculate the area of a regular polygon, in addition to the existing polygon-specific formulas, there is a formula that we can use for every regular polygon:
\(A=a⋅p\)
The → apothem
P → semiperimeter (half the perimeter)
Example:
A pentagon has sides of 4 cm and an apothem of 2.75 cm. What is the value of your area?
Resolution:
We know that:
\(A=a⋅p\)
Calculating the perimeter:
P = \(4⋅5\)
P = 20
So the semiperimeter is:
20: 2 = 10
So, to calculate the area, we have:
\(A=a⋅p\)
\(A=2.75⋅10\)
\(A=27.5\ cm^2\)
Difference between regular polygon and irregular polygon
A regular polygon is a polygon that is equilateral and equiangular at the same time. Otherwise, the polygon would be irregular. Then, An irregular polygon is one that does not have all sides congruent or all angles not congruent..
As the irregular polygon has at least one side with a different measure, the properties to find the measure of each interior angle or each exterior angle, for example, are not valid for the regular polygon.
Also access: Polyhedrons — the three-dimensional figures formed by joining regular polygons
Regular polygon exercises
A polygon that has 12 sides is known as a dodecagon. If this polygon is regular, the measure of each of its interior angles is:
A) 100°
B) 125°
C) 150°
D) 175°
E) 200°
Resolution:
Alternative C
Calculating the measure of each interior angle, we know that n = 12:
\(a_i=\frac{180⋅(12-2)}{12}\)
\(a_i=\frac{180⋅10}{12}\)
\(a_i=\frac{1800}{12}\)
\(a_i=150°\)
question 2
The polygon is considered regular if:
A) have parallel sides congruent to each other.
B) is an equilateral polygon.
C) is an equiangular polygon.
D) is an equilateral and equiangular polygon.
E) is a polygon with at least one side of different length.
Resolution:
Alternative D
A polygon is regular if it is both equilateral and equiangular, that is, if it has sides congruent to each other and angles congruent to each other.
By Raul Rodrigues de Oliveira
Maths teacher
Would you like to reference this text in a school or academic work? Look:
OLIVEIRA, Raul Rodrigues de. "Regular polygon"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/poligono-regular.htm. Accessed May 15, 2023.
Find out what the apothem of a polygon is and how to calculate its measure. Also know the main formulas for this calculation.
Learn to classify a polygon according to the number of sides. Also differentiate a convex polygon from a non-convex one and a regular one from an irregular one.
Click to learn what the elements of a polygon are and the properties they give to these flat geometric figures.
Diagonals of a polygon.
Learn what polygons are and what their elements are. Know the method of naming polygons and how we add the internal and external angles.
Get to know quadrilaterals and the basic characteristics that lead them to be classified as parallelograms, trapezoids or neither.
Click to learn how to calculate the sum of the interior and exterior angles of a convex polygon.
Learn to calculate the area of a square. Also know the formula to calculate the perimeter and diagonal of a square. See solved problems about square area.


