THE The internal bisector theorem was developed specifically for triangles and shows that when we trace the internal bisector of an angle of the triangle, the meeting point of the bisector with the side opposite to it divides that side into line segments proportional to the adjacent sides of that angle. With the application of the internal bisector theorem it is possible to determine the value of the side or segments of the triangle using the proportion between them.
See too: Median, angle bisector and height of a triangle — what's the difference?
Summary of the internal bisector theorem:
The bisector is a ray which divides the angle into two congruent angles.
The internal bisector theorem is specific to triangles.
This theorem proves that the bisector divides the opposite side into proportional segments to the sides adjacent to angle.
Video lesson on the internal bisector theorem
What is the bisector theorem?
Before we understand what the inner bisector theorem says, it is important to know what is
bisector of an angle. It is a ray that divides the angle into two congruent parts., that is, two parts that have the same measure.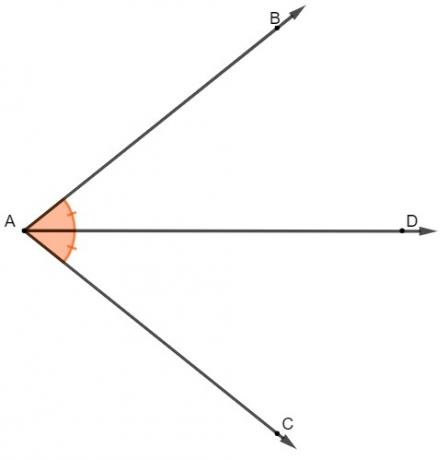
Understanding what the bisector is, we notice that it exists at the interior angle of a triangle. When we delineate the bisector of an angle of the triangle, it will divide the opposite side into two segments. Regarding the internal bisector, its theorem says that the two segments divided by it are proportional to the adjacent sides of the angle.
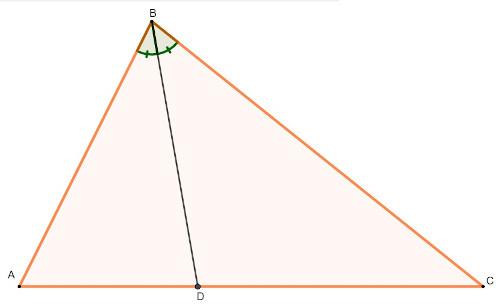
Note that the bisector divides the side AC into two segments, AD and DC. The bisector theorem shows that:
\(\frac{\overline{AB}}{\overline{AD}}=\frac{\overline{BC}}{\overline{CD}}\)
Know more: Pythagoras Theorem — another theorem developed for triangles
Proof of the internal bisector theorem
In triangle ABC below, we will demarcate the segment BD, which is the bisector of this triangle. Furthermore, we will trace the prolongation of its side CB and the segment AE, parallel to BD:
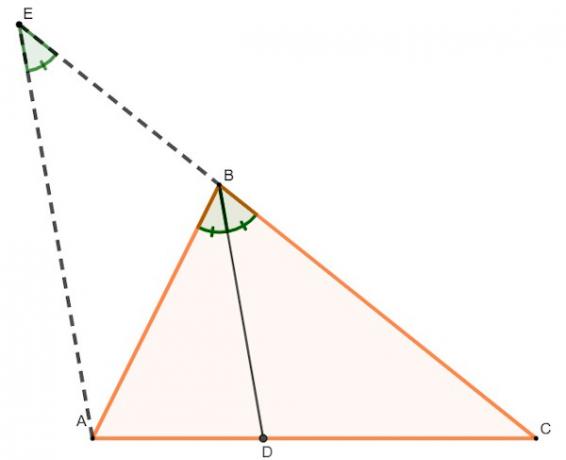
Angle AEB is congruent to angle DBC, because CE is a straight transversal to the parallel segments AE and BD.
applying the Thales' theorem, we concluded that:
\(\frac{\overline{BE}}{\overline{AD}}=\frac{\overline{BC}}{\overline{DC}}\)
Now we it remains to show that BE = AB.
Since x is the measure of the angle ABD and DBC, analyzing the angle ABE, we obtain:
ABE = 180 - 2x
If y is the measure of angle EAB, we have the following situation:

We know that the sum of the interior angles of the triangle ABE is 180°, so we can calculate:
180 - 2x + x + y = 180
– x + y = 180 – 180
– x + y = 0
y = x
If angle x and angle y have the same measure, triangle ABE is isosceles. Therefore, the side AB = AE.
Since the sum of the interior angles of a triangle is always equal to 180°, in triangle ACE we have:
x + 180 - 2x + y = 180
– x + y = 180 – 180
– x + y = 0
y = x
Since y = x, triangle ACE is isosceles. Therefore, the segments AE and AC are congruent. Swapping AE for AC in reason, it is proved that:
\(\frac{\overline{AB}}{\overline{AD}}=\frac{\overline{BC}}{\overline{DC}}\)
Example:
Find the value of x in the following triangle:
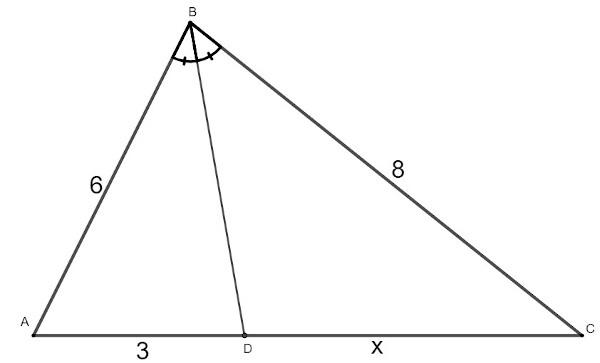
Analyzing the triangle, we obtain the following ratio:
\(\frac{6}{3}=\frac{8}{x}\)
Cross-multiplying:
6x = 8 ⋅ 3
6x = 24
\(x=\frac{24}{6}\)
x = 4
Read too: Notable Points of a Triangle — What Are They?
Solved exercises on the internal bisector theorem
question 1
Looking at the triangle below, we can say that the value of x is:
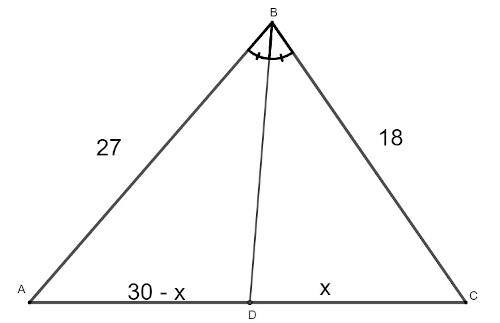
a) 9
B) 10
C) 11
D) 12
E) 13
Resolution:
Alternative D
Applying the internal bisector theorem, we get the following calculation:
\(\frac{27}{30-x}=\frac{18}{x}\)
Cross-multiplying:
\(27x=18\ \left (30-x\right)\)
\(27x\ =\ 540\ -\ 18x\ \)
\(27x\ +\ 18x\ =\ 540\ \)
\(45x\ =\ 540\ \)
\(x=\frac{540}{45}\)
\(x\ =\ 12\)
question 2
Analyze the following triangle, knowing that your measurements were given in centimeters.

The perimeter of triangle ABC is equal to:
A) 75 cm
B) 56 cm
C) 48 cm
D) 24 cm
E) 7.5 cm
Resolution:
Alternative C
Applying the bisector theorem, we will first find the value of x:
\(\frac{2x}{5}=\frac{4x-9}{7}\)
\(5\ \left (4x-9\right)=2x\cdot7\)
\(20x\ -\ 45\ =\ 14x\)
\(20x\ -\ 14x\ =\ 45\ \)
\(6x\ =\ 45\ \)
\(x=\frac{45}{6}\)
\(x\ =\ 7.5\)
Thus, the unknown sides measure:
\(2\cdot7,5\ =\ 15\ \)
\(4\cdot7,5\ -\ 9\ =\ 21\ \)
Remembering that the gauge length used was the cm, the perimeter of this triangle is equal to:
P = 21 + 15 + 5 + 7 = 48 cm
By Raul Rodrigues de Oliveira
Maths teacher
Source: Brazil School - https://brasilescola.uol.com.br/matematica/teorema-da-bissetriz-interna.htm

