O prism it is a geometric solid that we study in Spatial Geometry. In our daily lives, there are several objects that have a prism shape. A prism is a polyhedron that has two bases formed by polygons equal and rectangular side areas connecting the vertex of one base to its correspondent in the other base.
This polyhedron can be classified as straight or oblique, depending on its shape, because when inclined, it is known as an oblique prism. Otherwise it is a straight prism. The boxes, in general, have a prism shape, as well as buildings and other everyday elements.
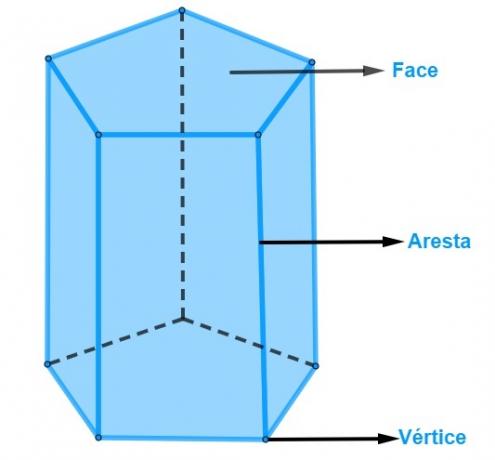
There are different types of prisms, as their base can be any polygon, there can be prisms with triangular, quadrangular, pentagonal, hexagonal bases, among others. The most common of them is the square-based prism, also known as paving stone rectangle. The main elements of a prism are its faces, vertices and edges. There are specific formulas for calculating the volume and total area of the prism.
Read too: How do you flatten a geometric solid?
prism summary
- A geometric solid is a prism when it has two identical polygonal bases and rectangular side areas connecting the vertex of one base to its counterpart on the other base.
- There are different prisms, such as the triangular-based prism, the quadrangular-based prism, among others.
- Several objects of our daily life have a prism shape, such as packaging.
- To calculate the lateral area of the prism, it is important to keep in mind that this depends on the polygon that forms the base of the prism. This calculation is done through the sum of the areas of existing rectangles or parallelograms, which individually are calculated by multiplication from the base by the height.
- To calculate the total area of the prism, we use the formula:
\(AT=2A_b+Al\)
- To calculate the volume of the prism, we use the formula:
\(V=A_b\cdot h\)
What are the elements of the prism?
just like the others polyhedra, the prism is composed of vertices, edges and faces, its main elements. It is worth noting that it has the characteristic side faces formed by parallelograms and bases formed by any polygons.
What bases can the prism have?
There are different types of prism depending on the shape of your base. There are prisms with triangular, square, quadrangular, pentagonal, hexagonal bases, among others. the prism can be formed by any base, as long as it is a polygon. See below for the main types of prism.

types of prisms
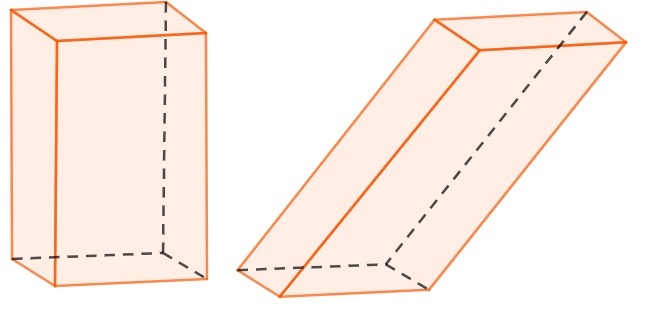
The prism can be considered a straight prism or an oblique prism.
- straight prism: occurs when the side edge forms a right angle to the prism bases.
- Oblique prism: occurs when the side edge does not form a right angle to the prism bases.
What are the prism formulas?
To calculate the lateral area, the total area and the volume of the prism, we use specific formulas. Let's see each of them below.
side area from the prism
The lateral area of the right prism is a rectangle and the oblique prism is a parallelogram. In both cases, we calculate the area by multiplying the base by the height, but the lateral area depends on the polygon that forms the base of the prism. Being \(TO 1\), \(A_2\),..., \(A_n\) the area of each side face of the prism with a base of no sides, the lateral area is given by:
\(A_l=A_1+A_2+...\ A_n\)
- Example:
Analyze the following prism and calculate its lateral area.

Resolution:
The lateral area of this prism is composed of 4 rectangles, 2 with sides measuring 4 cm and 10 cm and 2 with sides measuring 8 cm and 10 cm.
Thus, we can calculate the lateral area as follows:
\(A_l=2\cdot4\cdot10+2\cdot8\cdot10\)
\(A_l=80+160\)
\(H_l=240cm^2\)
See too: How is the area of the cylinder calculated?
Total area from the prism
Knowing the lateral area of the prism, we know that it has two equal bases, formed by polygons. So, to calculate the total area, it is necessary to calculate the base area plus side area.
\(AT=2Ab+Al\)
- Example:
From the analysis of the same prism used to calculate the lateral area, calculate the total area.
Resolution:
The total area is found by summing the areas of the bases and the lateral area. The bases are rectangles, and the area is equal to the product of the dimensions of the base. That is:
\(A_b=4\cdot8=32cm²\)
Therefore, the total area will be:
\(A_T=2A_b+A_l\)
\(A_T=2\cdot32+240\)
\(A_T=64+240\)
\(A_T=304\ cm^2\)
Video lesson on prism area
Volume from the prism
The volume of the prism is equal to the product of area of base and height, whether it is oblique or straight.
\(V=A_b·h\)
- Example:
From the analysis of the same prism used to calculate the lateral area and the total area, calculate the volume.
Resolution:
We know that its base is 32 cm². To calculate the volume, simply multiply the area of the base by the height, which is 10 cm. So, we have to:
\(V=A_b\cdot h\)
\(V=32\cdot10\)
\(V=320\ cm^3\)
Video lesson on prism volume
Solved exercises on prism
question 1
(Enem 2017) A hotel chain has simple cabins on the island of Gotland, Sweden, as shown in Figure 1. The support structure of each of these huts is represented in Figure 2. The idea is to allow the guest a stay free of technology, but connected with nature.
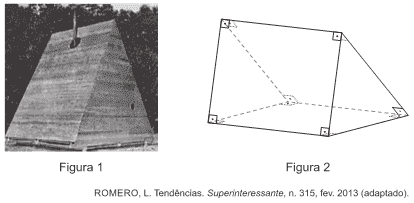
The geometric shape of the surface whose edges are shown in Figure 2 is
- tetrahedron.
- rectangular pyramid.
- rectangular pyramid trunk.
- right quadrangular prism.
- straight triangular prism.
Resolution:
Alternative D
Analyzing the Geometric form, you can see that it is composed of two triangular faces and that the other faces are rectangles. So this is a right quadrangular prism.
question 2
Analyze the following statements and judge them as true or false:
I – Pyramids are not considered prisms.
II – There is a prism with a circular base, also known as a cylinder.
III – Every prism has rectangular side faces.
Is/are correct(s):
A) only statement I.
B) only statement II.
C) only statement III.
D) only statements I and III.
E) all statements.
Resolution:
Alternative A
I - True
We know that the pyramid it has triangular side faces and only one base, so it is not a prism.
II - False
The cylinder cannot be considered a prism. For a shape to be a prism, its base must be a polygon. The circle is not a polygon.
III - False
When the prism is oblique, its side face is formed by parallelograms, not rectangles.