THE paving stone it is a geometric solid which has three dimensions: height, width and length. This prism has all its faces in the shape of a parallelogram, being formed by 6 faces, 8 vertices and 12 edges. It is a very common geometric shape in our daily lives, seen, for example, in shoe boxes, in the shape of some swimming pools, etc. The volume of a parallelepiped is calculated by the product of the length of its three dimensions. Their total area is equal to the sum of the areas of their faces.
Read too: Flattening of geometric solids — the representation of their faces in two-dimensional form
Summary about cobblestone
The parallelepiped is a geometric solid formed by faces in the shape of parallelograms.
It consists of 6 faces, 8 vertices and 12 edges.
It can be oblique or straight.
To calculate the volume of a parallelepiped, we calculate the product of the height, width and length of the cobblestone.
The total area of a parallelepiped is calculated by AT = 2ab + 2ac + 2bc.
Video lesson on cobblestone
Features of the cobblestone
A parallelepiped is a geometric solid that has faces formed by parallelograms. This format is quite common in our daily lives, being a particular case of prisms, as prisms are geometric solids that havetwo congruent bases. To be characterized as parallelepipeds, therefore, the bases are formed by parallelograms. Thus, the parallelepiped has 6 faces formed by parallelograms, 8 vertices and 12 edges. See below:

Classification of the cobblestone
There are two possible classifications for a cobblestone:
straight cobblestone: when the edges of the side faces are perpendicular to the base.
Oblique parallelepiped: when the side edges are oblique to the base.

cobblestone formulas
There are specific formulas for calculating the volume, total area, and diagonal length of a straight parallelepiped. The oblique parallelepiped does not have specific formulas for these calculations, as it mainly depends on:
the shape of its base;
of its inclination.
In addition to these, it depends on several other factors that are studied further in Higher Education. In our daily life, the most recurrent is the straight parallelepiped, also known as rectangular parallelepiped. See below how to calculate its volume, area and diagonal.
cobblestone volume
To calculate the volume of a parallelepiped, it is enough to make the multiplication length, width and height of this geometric solid.
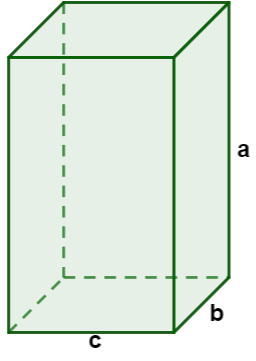
To calculate the volume of the parallelepiped, we use the following formula:
\(V=a\cdot b\cdot c\)
→ Example of calculating the volume of the parallelepiped
A box is shaped like a straight parallelepiped, 10 cm high, 6 cm wide and 8 cm wide. What is the volume of this box?
Resolution:
To calculate the volume, we will multiply the three given dimensions, that is:
\(V=a\cdot b\cdot c\)
\(V=10\cdot6\cdot8\)
\(V=60\cdot8\)
\(V=480\ cm^3\)
Therefore, the volume of this box is 480 cm³.
Know more: Volume Measurements — What Are They?
cobblestone area
The area of a geometric solid and thesum of the areas of your faces. A parallelepiped has 6 faces. Furthermore, analyzing this solid, it is possible to see that the opposite faces are congruent. In a straight parallelepiped, the faces are formed by rectangles. Thus, to calculate the area of each of the faces, simply multiply the two dimensions of the face.
To calculate the total area of the parallelepiped, we use the following formula:
\(A_T=2ab+2ac+2bc\)
→ Example of calculating the area of the parallelepiped
Calculate the total area of the following parallelepiped:
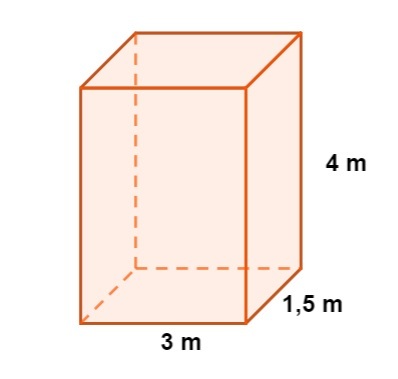
Resolution:
Calculating the total area, we have:
\(A_T=2\cdot4\cdot1,5+2\cdot4\cdot3+2\cdot3\cdot1,5\)
\(A_T=12+24+9\)
\(A_T=45m^2\)
So the total area of this cobblestone is 45 m².
Diagonal of the parallelepiped
When we draw the diagonal of a parallelepiped, it is also possible to calculate its length. For this, it is necessary to know the measure of this geometric solid.
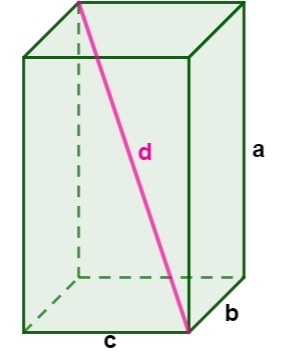
To calculate the length of the diagonal of the parallelepiped, we use the following formula:
\(d=\sqrt{a^2+b^2+c^2}\)
→ Example of calculating the diagonal of the parallelepiped
What is the length of the diagonal of a parallelepiped that is 6 cm high, 6 cm wide, and 7 cm long?
Resolution:
Calculating the length of the diagonal, we have:
\(d=\sqrt{6^2+6^2+7^2}\)
\(d=\sqrt{36+36+49}\)
\(d=\sqrt{121}\)
\(d=11 cm\)
Also know: Diagonals of a polygon — how to calculate their quantity?
Solved exercises on cobblestone
question 1
(Integrated Technician - IFG) The internal measurements of a reservoir in the shape of a parallelepiped are 2.5 m long, 1.8 m wide and 1.2 m deep (height). If, at a given time of day, this reservoir is only at 70% of its capacity, the amount of liters that are needed to fill it is equal to:
A) 1620
B) 1630
C) 1640
D) 1650
E) 1660
Resolution:
Alternative A
To calculate the volume, we will multiply the dimensions:
\(V=\mathrm{2,5}⋅1{,8}\cdot\mathrm{1,2}\)
\(V=\mathrm{5.4}m\)
To convert the capacity from 5.4 m³ to liters, it is necessary to convert the unit of capacity measure, multiplying by 1000, that is:
V = 5.4 · 1000 = 5400 liters
We know that 70% of the reservoir is full, leaving 30% of that capacity to finish filling it. So the missing amount is:
30% of 5400 = 0.3 · 5400 = 1620 liters
question 2
A rectangular block has a diagonal measuring 12.5 cm, a height of 7.5 cm and a width of 8 cm. The length of this block is:
A) 5 cm
B) 6 cm
C) 7 cm
D) 9 cm
E) 10 cm
Resolution:
Alternative B
Using the diagonal formula, we have:
\(d=\sqrt{a^2+b^2+c^2}\)
\(\mathrm{12,5}=\sqrt{{\mathrm{7,5}}^2+8^2+c^2}\)
\({\mathrm{12,5}}^2=\sqrt{{\mathrm{56,25}+64+c^2}^2}\)
\(\mathrm{156.25}=\mathrm{56.25}+64+c^2\)
\(\mathrm{156.25}-\mathrm{56.25}-64=c^2\)
\(100-64=c^2\)
\(36=c^2\)
\(c=\sqrt{36}\)
\(c=6 cm\)


