THE Plane Geometry It is present at all times in our daily lives. When we look at the world around us, it is possible to notice various geometric shapes. When geometric shapes have two dimensions, they are the object of study of Plane Geometry..
The point, the line and the plane are primitive elements studied in Plane Geometry, in addition to the notions of angles and the study of flat figures, such as the square, triangle, rectangle, trapezoid, circle, and rhombus. In addition to plane geometry, there is also Spatial Geometry, another area of Math, which studies three-dimensional geometric figures. The study of Plane Geometry is essential to understand the space in which we live.
Know more: Analytical Geometry — area that studies Geometry using algebraic tools
Summary of Plane Geometry
Plane Geometry is the area of Mathematics that studies plane figures.
Point, line and plane are the primitive concepts of this geometry.
-
There are important concepts that are the basis of Plane Geometry and that are developed from the primitive concepts.
ray: is the part of a line bounded by a point.
Line segment: the part of a line bounded by two points.
Angle: is the region between two rays.
polygons: are plane figures enclosed by rays.
Area: is the measurement of the surface of a plane figure.
Many plane figures are studied in plane geometry, such as the triangle, parallelogram, rectangle, rhombus, square, trapezoid, circumference, and circle.
There are important formulas for calculating the measurements of each of the plane figures, such as the perimeter, which is the sum of the contour of the figure, and the calculation of the area:

Video lesson on Plane Geometry
Important concepts of Plane Geometry
In the study of plane geometry, important concepts were developed, starting with the primitive concepts, which are those of point, line and plane. These objects are known as primitives because they are the basis for the development of other concepts, such as angle, ray, line segment, polygon, area, etc. Let's look at each of them.
Point, line and plane
The point, line and plane are primitive elements of mathematics, that is, they have no definition, but are objects that are in our imagination, understood intuitively, and are essential for the construction of the concepts of Plane Geometry.
THE point is the simplest object in geometry. It has no dimension, that is, it is dimensionless, and helps us to find locations in the plane accurately. Its use is common to represent a GPS location in applications, for example.
THE line, in turn, is formed by a set of points that are aligned. In a plane, there are points that are on the line and outside the line. It has only one dimension, with negligible width and depth. The lines are infinite and can be the representation of a trajectory in the plane.
THE plane is a surface that has no curves, that is, it is a two-dimensional region. The plane is infinite for both dimensions, and in it we can insert infinite lines. When we imagine a line, we know that it is contained in a certain surface, which is the plane.
To represent and name these primitive elements, we use the following notations:
The point is represented by a capital letter of our alphabet, such as A, B, C.
The line is represented by a lowercase letter of the alphabet, such as r, s, t.
The plane is represented by a Greek letter of the alphabet, such as α, β.

Ray and line segment
Based on these basic concepts, it is possible to understand important concepts such as ray and line segment. A ray is the part of a straight line that has a beginning but no end..To represent a ray, we use two points — the first is the starting point of the ray and the second is any point belonging to it. With an indicative arrow above the two letters that represent points, it is shown that a ray starts at point A and passes through point B: .
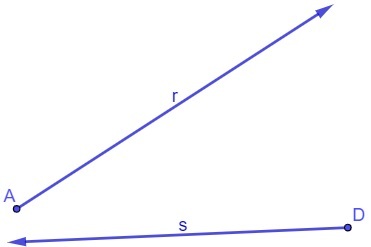
Additionally, there is the line segment, which is also part of a line, but has a certain beginning and end. The line segment is usually represented by the letters of the points that limit it with a dash above it. For example, .

Angle
Understanding well the concepts involving line, ray and line segment, it is possible to understand the idea of angle. The region between the lines will be known as angle whenever there is two lines meet at a point called a vertex.
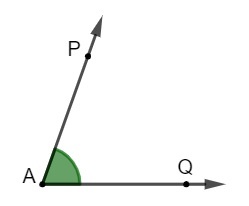
Classification of angles
According to the measure of the angles, it is possible to classify them as:
acute angle: if the measurement is less than 90°;
Straight angle: if the measurement is equal to 90°;
obtuse angle: if the measurement is greater than 90° and less than 180°;
Shallow angle: if the measurement is equal to 180°.
Read too: Complementary and Supplementary Angles—What Does Each Mean?
Plane Geometry figures and formulas to calculate their measurements
the flat figures are the geometric figures represented on a plane. Some of the flat figures were studied in depth, generating important concepts, such as area and perimeter. In addition, each of the figures has its characteristics studied.
Relative to a plane figure, the area is the measurement of its surface and the perimeter is the length of the contour of the figure, that is, the sum of the length from your sides. See below for the main plane figures and formulas for calculating their area and perimeter.
triangles
we know how triangle the flat figure that has three sides. To find the value of its area, we calculate the product of the base length, the height length and divide by 2. Its perimeter is found by adding the sides.

parallelogram
we know how parallelogram the flat figure that has four parallel sides two by two. To find the value of the area of a parallelogram, simply calculate the product of its base and height. Its perimeter is found by adding all of its sides. Since the parallel sides are congruent, the formula for calculating the perimeter of the parallelogram is the sum of the base and the oblique side multiplied by 2.

Rectangle
The rectangle is a four-sided flat figure that has all right angles. To calculate the area of a rectangle, we multiply the base by the height. The value of the perimeter is equal to the sum of its sides. Since this figure has congruent sides two by two, there is a formula to calculate its perimeter, which is the sum of the longer side and the longer side multiplied by 2.

Also know: Polyhedron — any geometric solid whose faces are formed by polygons
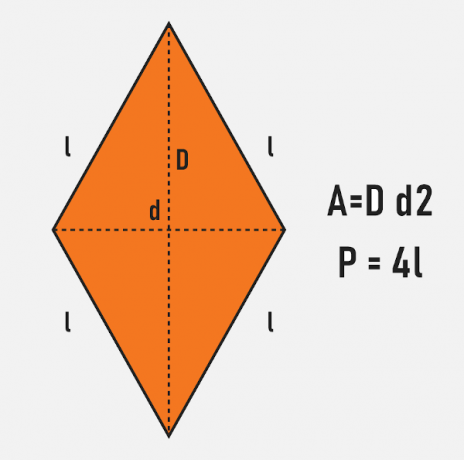
Diamond
THE diamond is a flat figure that, unlike the previous ones, has four congruent sides. To calculate its area it is necessary to find the length of its diagonals, where D represents the major diagonal and d the minor diagonal. Since all sides are congruent, to calculate the perimeter of the rhombus, simply multiply the length of the side by 4.
Square
THE square is a special case of rhombus and rectangle, because it has all 4 sides congruent and also has all angles congruent. To calculate its area, simply multiply its base by its height. Since the sides are congruent, just calculate the square of the side. Thus, this figure, like the trapezoid, has all congruent sides. Therefore, its perimeter is calculated when we multiply the length of the side by 4.

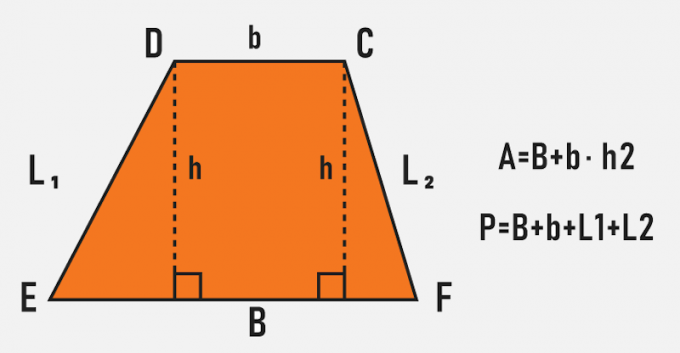
trapeze
The trapeze is a quadrilateral what has two parallel sides and the other two non-parallel sides. To calculate its area, it is necessary to know the length of the larger base, the smaller base and the height. To find its perimeter, there is no specific formula, which is calculated by adding its bases to the oblique sides.
Circumference and circle
THE circumference is the figure formed by the set of points that are the same distance (r) from a point known as the center.
The circle is the region bounded by the circumference.
To calculate the area and circle length, we use the following formulas:

Difference between Plane Geometry and Spatial Geometry
As we have seen, Plane Geometry is the study of geometric figures and objects on the plane. It is restricted, then, to two dimensions. In it, plane figures are studied, such as the square, the rectangle and the triangle. Already Spatial Geometry studies elements in a three-dimensional universe. Then, we studied the Geometric solids, which are the cube, the pyramids, the sphere, among others. Plane Geometry is the basis for the study of Spatial Geometry.
Also access: Difference between circumference, circle and sphere — tips to never go wrong again
Solved exercises on Plane Geometry
question 1
A football field is 70 meters wide and 110 meters long. If during warm-up an athlete completes 10 laps on this field, he will walk a total of:
A) 180 meters
B) 360 meters
C) 1800 meters
D) 3600 meters
E) 7200 meters
Resolution:
Alternative D
First, we will calculate the perimeter of this plot:
P = 2 (70 + 110)
P = 2 · 180
P = 360
As he completed 10 laps then:
360 · 10 = 3600 meters
question 2
A square has a circular shape, with a radius of 8 meters. Using π = 3, the area of this square is:
A) 158 m²
B) 163 m²
C) 192 m²
D) 210 m²
E) 250 m²
Resolution:
Alternative C
Calculating the area, we have:
A = πr²
A = 3 · 8²
A = 3 · 64
A = 192 m²

