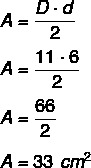THE area of a plane figure is the measurement of the surface of this figure. The calculation of the area is of great importance to solve certain situations involving plane figures. each of flat figures has a specific formula for calculating area. THE area is studied in plane geometry, since we calculate the area of two-dimensional figures.
Read too: Difference between circumference, circle and sphere
Formulas and how to calculate the area of the main plane figures
triangle area
THE triangle is the simplest polygon in plane geometry, as it is composed by 3 sides and 3 angles, being the polygon with fewer sides. As our objective is to calculate the area of the triangle, it is important to know how to recognize its base and height.
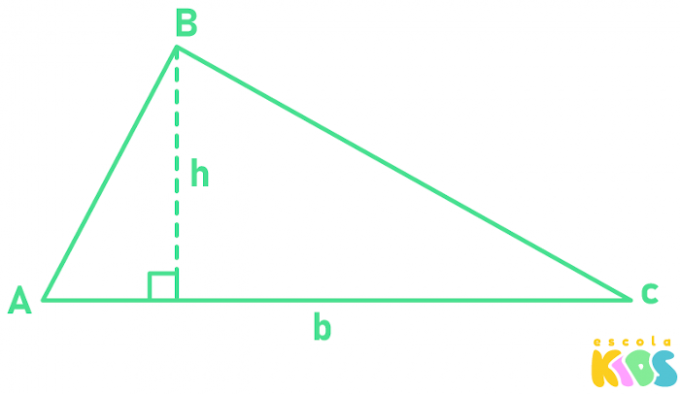
THE triangle area is equal to product of base and height divided by 2.

b → base length
h → height length
Example:
What is the area of a triangle whose base is 10 cm and height is 9 cm?
Resolution:

square area
THE square it is a polygon that has 4 sides. It is considered a regular polygon because it has all sides and
angles congruent to each other, that is, the sides have the same measure, as well as the angles. The most important element in the square for calculating the area is its side.
In any square, to calculate its area, it is necessary to know the measure of one of its sides:
A = l2
l → side length
Example:
What is the area of a square whose sides are 6 cm long?
Resolution:
A = l2
A = 62
H = 36 cm2
rectangle area
THE rectangle It gets its name because it has right angles. And the 4-sided polygon I havei all congruent angles and measuring 90°. To calculate the area of the rectangle, first, it is necessary to know its base and its height.

To find the area of the rectangle, just calculate the product between the base and the height of the figure.
A = b · h
b → base
h → height
Example:
A rectangle has sides measuring 12 cm and 6 cm, so what is its area?
Resolution:
We know that b = 12 and c = 6. Substituting into the formula, we have:
A = b · h
A = 12 ·6
H = 72 cm2
diamond area
THE diamond also has 4 sides, but all are congruent. To calculate the rhombus area, it is necessary to know the length of its diagonals, the major diagonal and the minor diagonal.
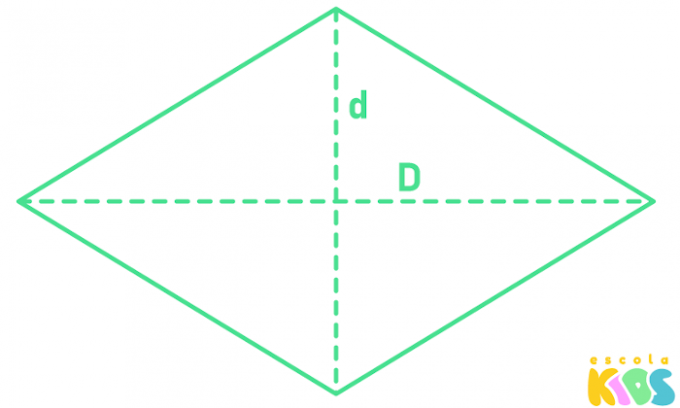
The area of the rhombus is equal to the product of the lengths of the major and minor diagonals divided by 2.
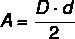
D → length of the longest diagonal
d → length of the smaller diagonal
Example:
A rhombus has a smaller diagonal equal to 6 cm and a larger diagonal equal to 11 cm, so its area is equal to:
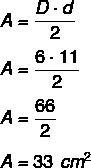
trapeze area
The last quadrilateral is the trapezoid, it has two parallel sides, known as major base and minor base, and two non-parallel sides. To calculate the area of a trapezoid, it is necessary to know the length of each base and the length of its height.
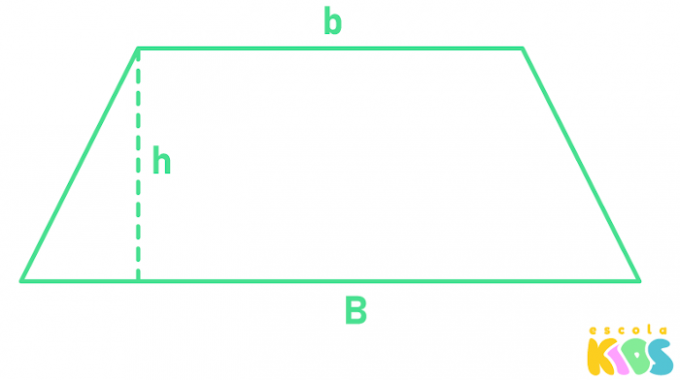

B → larger base
b → minor base
h → height
Example:
What is the area of a trapezoid that has a greater base of 8 cm, a smaller base of 4 cm and a height of 3 cm?
Resolution:

circle area
The circle is formed by the region that is contained within a circumference, which is the set of points that are the same distance from the center. THE The circle's main element for area calculation is its perimeter.

A = πr2
r → radius
π is a constant used for calculations involving circles. as it is a irrational number, when we want the area of the circle, we can use an approximation to it, or simply use the symbol π.
Example:
Find the area of a circle of radius r = 5 cm (use π = 3.14).
Resolution:
Substituting into the formula, we have:
A = πr2
A = 3.14 · 52
A = 3.14 · 25
H = 78.5 cm2
Video lesson on areas of plane figures
Read too: Congruence of geometric figures — what are the criteria?
Solved exercises on areas of plane figures
question 1
(Enem) A cell phone company has two antennas that will be replaced by a new, more powerful one. The coverage areas of the antennas that will be replaced are circles of radius
2 km, whose circumferences touch each other at point O, as shown in the figure.

Point O indicates the position of the new antenna, and its coverage region will be a circle whose circumference will externally tangent to the circumferences of the smaller coverage areas.
With the installation of the new antenna, the measurement of the coverage area, in square kilometers, was increased by
a) 8π.
B) 12π.
C) 16π.
D) 32π.
E) 64π.
Resolution:
Alternative A
In the image it is possible to identify 3 circles; the 2 smaller ones have a radius of 2 km, so we know that:
THE1 = πr2
THE1 = π ⸳ 22
THE1 = 4 π
As there are 2 smaller circles, so the area they occupy together is 8 π.
Now we will calculate the area of the larger circle, which has a radius of 4 km:
THE2 = πr2
THE2 = π⸳ 42
THE2 = 16 π
Calculating the difference between the areas, we have 16π– 8π = 8 π.
question 2
A rhombus has a smaller diagonal (d) measuring 6 cm and a larger diagonal (D) measuring twice the larger diagonal minus 1, so the area of this rhombus is equal to:
A) 33 cm2
B) 35 cm2
C) 38 cm2
D) 40 cm2
E) 42 cm2
Resolution:
Alternative A
Knowing that d = 6, then we have that D = 2 · 6 – 1 = 12 – 1 = 11 cm. Calculating the area, we have: