Trigonometric ratios: sine, cosine and tangent are relations between the sides of a right triangle. Using these ratios it is possible to determine unknown values of angles and side measurements.
Practice your knowledge with the resolved issues.
questions about sine
question 1
being the angle equal to 30° and the hypotenuse 47 m, calculate the height measurement The of the triangle.

The trigonometric sine ratio is the quotient between the measures of the opposite side of the angle, and the hypotenuse.
Isolating The on the one hand of equality, we have:
From a trigonometric table, we have that sine of 30° is equal to , substituting in the equation:
Therefore, the height of the triangle is 23.50 m.
question 2
The top view of a park shows two paths to get to point C from point A. One of the options is to go to B, where there are drinking fountains and resting places, and then to C. If a visitor to the park wants to go straight to C, how many meters will he have walked less than the first option?
Consider approximations:
sin 58° = 0.85
cos 58° = 0.53
tan 58° = 1.60
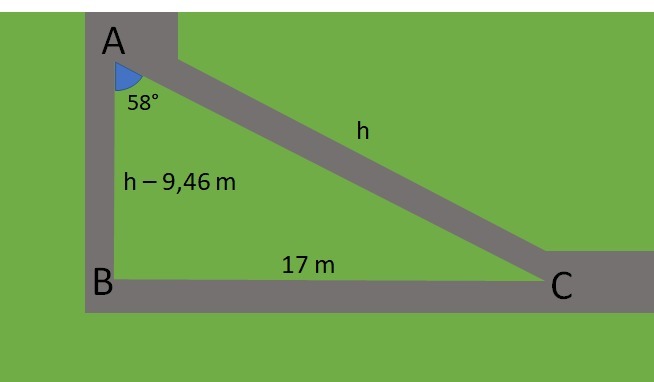
Answer: leaving A and going straight to C, the walk is 7.54 m shorter.
Step 1: calculate distance.
Step 2: determine the distance.
Step 3: determine the distance .
Step 4: Determine the difference between the two paths.
question 3
A cable car was installed connecting a base to the top of a mountain. For the installation, 1358 m of cables were used, arranged at an angle of 30° in relation to the ground. How high is the mountain?

Correct answer: the height of the mountain is 679 m.
We can use the sine trigonometric ratio to determine the height of the mountain.
From a trigonometric table, we have sin 30° = 0.5. As the sine is the ratio between the opposite side and the hypotenuse, we determine the height.
question 4
(CBM-SC, soldier-2010) To help a person in an apartment during a fire, firefighters will use a 30m ladder, which will be placed as shown in the figure below, forming an angle with the ground of 60th. How far is the apartment from the floor? (Use sen60º=0.87; cos60º=0.5 and tg60º= 1.73)

a) 15 m.
b) 26.1 m.
c) 34.48 m.
d) 51.9 m.
Correct answer: b) 26.1 m.
To determine the height, we will use the 60° sine. Calling the height h and using 60° sine equal to 0.87.
Questions about cosine
question 5
Cosine is the ratio between the side adjacent to an angle and the measurement of the hypotenuse. Being equal to 45°, calculate the measure of the leg adjacent to the angle alpha, in the triangle of the figure.
consider

Approximating the square root value of 2:
The measure of the adjacent leg is approximately 19.74 m.
question 6
During a football match, player 1 throws to player 2 at a 48° angle. How far must the ball travel to reach player 2?
Consider:
sin 48° = 0.74
cos 48° = 0.66
tan 48° = 1.11
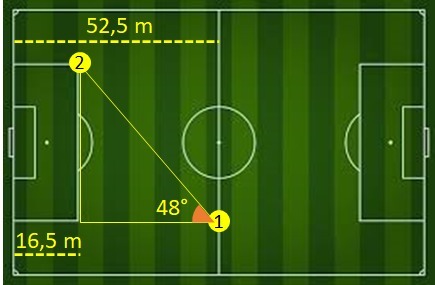
Correct answer: The ball must travel a distance of 54.54 m.
The measurement between player 1 and player 2 is the hypotenuse of the right triangle.
The cosine of the 48° angle is the ratio of its adjacent side to the hypotenuse, where the adjacent side is the distance between the midfield and the large area.
52.5 - 16.5 = 36 m
Calculating the cosine, where h is the hypotenuse.
question 7
A roof is considered to be gable when there are two slopes. In one work, a roof is being built where the meeting of its two waters is exactly in the middle of the slab. The angle of inclination of each water in relation to the slab is 30°. The slab is 24 m long. To order the tiles even before the structure that will support the roof is completed, it is necessary to know the length of each water, which will be:
As the slab is 24 m long, each water will be 12 m.
Calling the length of each roof water L, we have:
Rationalizing the fraction to get the irrational number of the denominator.
Making,
Therefore, the length of each roof water will be approximately 13.6 m.
question 8
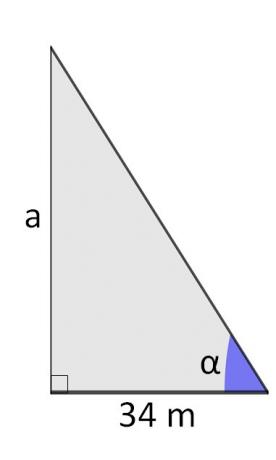
Tangent is the ratio between the side opposite an angle, and its adjacent side. being the angle equal to 60°, calculate the height of the triangle.
Tangent questions
question 9
A person wants to know the width of a river before crossing it. For this, it sets a reference point on the other edge, like a tree for example (point C). In the position you are in (point B), walk 10 meters to the left, until an angle of 30° is formed between point A and point C. Calculate the width of the river.
consider .

To calculate the width of the river that we will call L, we will use the tangent of the angle .
question 10
(Enem 2020) Pergolado is the name given to a type of roof designed by architects, commonly in squares and
gardens, to create an environment for people or plants, in which there is a drop in the amount of light,
depending on the position of the sun. It is made as a pallet of equal beams, placed parallel and perfectly
in a row, as shown in the figure.
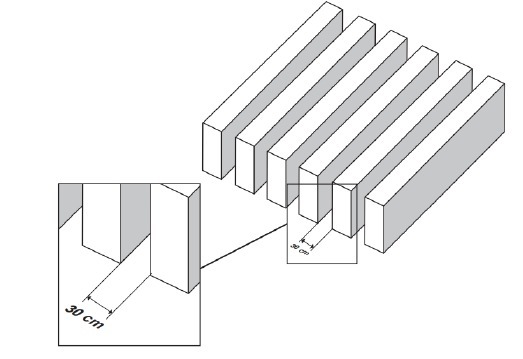
An architect designs a pergola with 30 cm spans between its beams, so that, in the
summer solstice, the trajectory of the sun during the day is carried out in a plane perpendicular to the direction of
beams, and that the afternoon sun, when its rays make 30° with the pin position, generate half
of the light that passes in the pergola at noon.
To meet the project proposal prepared by the architect, the pergola beams must be
constructed so that the height, in centimeters, is as close as possible to
a) 9.
b) 15.
c) 26.
d) 52.
e) 60.
Correct answer: c) 26.
To understand the situation, let's make an outline.

The image on the left shows the incidence of sunlight at midday, with 100%. The image on the left is what interests us. It allows only 50% of the sun's rays to pass through the pergola at a 30% slope.
We use the tangent trigonometric ratio. The tangent of an angle is the ratio of the opposite side to the adjacent side.
Calling the height of the pergola piece h, we have:
Making a tangent of 30° =
Let's rationalize the last fraction so that we don't leave the root of three, an irrational number, in the denominator.
Making,
Of the options available for the question, the closest one is the letter c, the height of the beams must be approximately 26cm.
question 11
(Enem 2010) An atmospheric balloon, launched in Bauru (343 kilometers northwest of São Paulo), at night last Sunday, it fell this Monday in Cuiabá Paulista, in the Presidente Prudente region, scaring
farmers in the region. The artifact is part of the Hibiscus Project program, developed by Brazil, France,
Argentina, England and Italy, to measure the behavior of the ozone layer, and its descent took place
after compliance with the expected measurement time.

On the date of the event, two people saw the balloon. One was 1.8 km from the balloon's vertical position
and saw it at an angle of 60°; the other was 5.5 km from the balloon's vertical position, aligned with the
first, and in the same direction, as seen in the figure, and saw it at an angle of 30°.
What is the approximate height of the balloon?
a) 1.8 km
b) 1.9 km
c) 3.1 km
d) 3.7 km
e) 5.5 km
Correct answer: c) 3.1 km
We use the 60° tangent which is equal . The tangent is the trigonometric ratio between the opposite side of the angle and its adjacent one.
Therefore, the height of the balloon was approximately 3.1 km.

