An polynomial equation is characterized by having a polynomial equal to zero. It can be characterized by the degree of the polynomial, and the greater this degree, the greater the degree of difficulty in finding its solution or root.
It is also important, in this context, to understand what the fundamental theorem of algebra is, which states that every polynomial equation has at least one complex solution, in other words: an equation of degree one will have at least one solution, an equation of degree two will have at least two solutions, and so on.
Read too: What are the classes of polynomials?
What is a Polynomial Equation
A polynomial equation is characterized by having a polynomial equal to zero, thus, every expression of type P(x) = 0 is a polynomial equation, where P(x) is a polynomial. Below is the general case of a polynomial equation and some examples.
Consider theno, an -1, a n -2, …, The1, a0 and x real numbers, and n is a positive integer, the following expression is a polynomial equation of degree n.

- Example
The following equations are polynomials.
a) 3x4 + 4x2 – 1 = 0
b) 5x2 – 3 = 0
c) 6x – 1 = 0
d) 7x3 – x2 + 4x + 3 = 0
Like polynomials, polynomial equations have their degree. To determine the degree of a polynomial equation, just find the highest power whose coefficient is different from zero. Therefore, the equations of the previous items are, respectively:
a) The equation is from fourth degree:3x4+ 4x2 – 1 = 0.
b) The equation is from high school:5x2 – 3 = 0.
c) The equation is from first degree:6x – 1 = 0.
d) The equation is of the third degree: 7x3– x2 + 4x + 3 = 0.
How to solve a polynomial equation?
The method of solving a polynomial equation depends on its degree. The greater the degree of an equation, the more difficult it is to solve it. In this article, we will show the solving method for polynomial equations of the first degree, second degree and bisquare.
Polynomial Equation of the First Degree
A polynomial equation of the first degree is described by a degree 1 polynomial. So we can write an equation of the first degree, in general, as follows.
Consider two real numbers The and B with a ≠ 0, the following expression is a polynomial equation of the first degree:
ax + b = 0
To solve this equation, we must use the equivalence principle, that is, everything that is operated on one side of equality must also be operated on the other side. To determine the solution of an equation of the first degree, we must isolate the unknown. For this, the first step is to eliminate the B on the left side of the equality, and then subtractoars b on both sides of the equality.
ax + b - B = 0 - B
ax = - b
Note that the value of the unknown x is not isolated, the coefficient a needs to be eliminated from the left side of the equality, and for that, let's divide both sides by The.
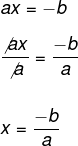
- Example
Solve the equation 5x + 25 = 0.
To solve the problem, we must use the equivalence principle. In order to facilitate the process, we will omit the writing of the operation on the left side of the equality, being equivalent then to say that we are going to “pass” the number to the other side, changing the sign (inverse operation).
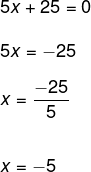
Learn more about solving this type of equation by accessing our text: First degree equation with an unknown.
Polynomial Equation of the Second Degree
A polynomial equation of the second degree has the characteristic of a degree two polynomial. So, consider a, b, and c real numbers with a ≠ 0. A second degree equation is given by:
ax2 + bx + c = 0
Your solution can be determined using the method of bhaskara or by factoring. If you want to know more about equations of this type, read: Eqaction of ssecond grau.
→ Bhaskara Method
Using Bhaskara's method, its roots are given by the following formula:

- Example
Find the solution of the equation x2 – 3x + 2 = 0.
Note that the coefficients of the equation are, respectively, a = 1, b = – 3 and c = 2. Replacing these values in the formula, we have to:
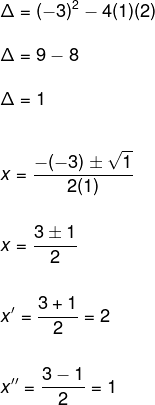
→ Factorization
See that it is possible to factor the expression x2 – 3x + 2 = 0 using the idea of polynomial factorization.
x2 – 3x + 2 = 0
(x – 2) · (x – 1) = 0
Notice now that we have a product equal to zero, and a product equals zero only if one of the factors equals zero, so we have to:
x – 2 = 0
x = 2
or
x - 1 = 0
x = 1
See that we found the solution to the equation using two different methods.
bi-square equation
THE bisquare equation it is a particular case of a polynomial equation of the fourth degree, normally a fourth degree equation would be written in the form:
ax4 + bx3 + box2 + dx + e = 0
where the numbers a B C D and and are real with a ≠ 0. A fourth degree equation is considered bisquare when the coefficients b = d = 0, that is, the equation is in the form:
ax4 + box2 + and = 0
See, in the example below, how to solve this equation.
- Example
Solve the x equation4 – 10x2 + 9 = 0.
To solve the equation, we're going to use the following unknown change, and whenever the equation is bisquare, we're going to make that change.
x2 =p
From the bi-square equation, notice that x4 = (x2)2 and therefore we have to:
x4 – 10x2 + 9 = 0
(x2)2 – 10x2 + 9 = 0
for2 – 10p + 9 = 0
See that we now have a polynomial equation of the second degree and we can use Bhaskara's method, like this:
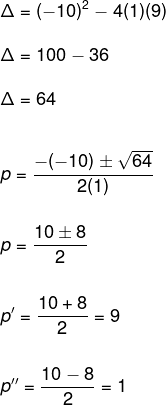
However, we must remember that, at the beginning of the exercise, an unknown change was made, so we must apply the value found in the substitution.
x2 =p
For p = 9 we have that:
x2 = 9
x’ = 3
or
x’’ = – 3
For p = 1
x2 = 1
x’ = 1
or
x’’ = – 1
Therefore, the solution set of the bisquare equation is:
S = {3, –3, 1, –1}
Read too: Briot-Ruffini's practical device – division of polynomials
Fundamental Theorem of Algebra (TFA)
The fundamental theorem of algebra (TFA), proved by Gauss in 1799, states that every polynomial equation as follows has at least one complex root.
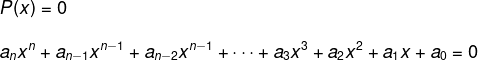
The root of a polynomial equation is its solution, that is, the unknown value is what makes the equality true. For example, a first-degree equation has a root already determined, as does a second-degree equation, which has at least two roots, and a bisquare, which has at least four roots.
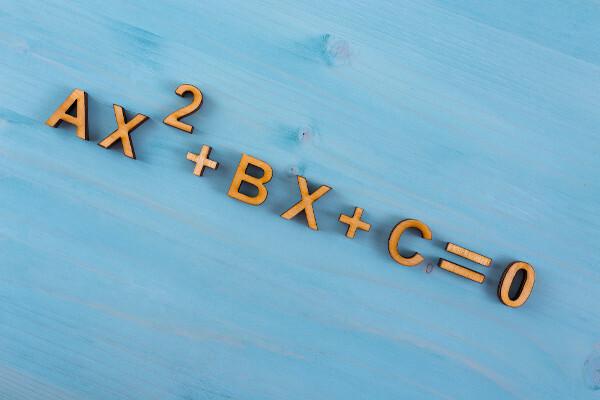
solved exercises
question 1 – Determine the value of x that makes the equality true.
2x – 8 = 3x + 7
Resolution
Note that to solve the equation, it is necessary to organize it, that is, leave all the unknowns on the left side of the equality.
2x – 8 = 3x + 7
2x – 3x = 7 + 8
– x = 15
By the equivalence principle, we can multiply both sides of the equality by the same number, and since we want to find the value of x, we will multiply both sides by –1.
(–1)– x = 15(–1)
x = – 15
question 2 – Marcos has R$ 20 more than João. Together, they manage to buy two pairs of sneakers, costing R$80 each pair and with no money left. How many reais have John?
Resolution
Assume that Mark has x reais, as John has 20 reais more, so he has x + 20.
Marks → x reals
João → (x + 20) reais
how did they buy two pairs of sneakers which cost 80 reais each, so if we put the parts of each one together, we will have to:
x + (x + 20) = 2 · 80
x + x = 160 – 20
2x = 140

Therefore, Mark had 70 reais, and João, 90 reais.
by Robson Luiz
Maths teacher
Source: Brazil School - https://brasilescola.uol.com.br/matematica/equacao-polinomial.htm
