Newton's binomial: what is it, formula, examples

Newton's binomial is any binomial raised to a number no on what no it's a natural number. Thanks to the studies of the physicist Isaac Newton about the powers of binomials, it was possible check regularities that facilitate the representation of the polynomial generated from the power of a binomial.

Observing these regularities, it also became possible find only one of the terms of polynomial, without having to calculate it all, using the formula of the general term of a binomial. In addition, Newton noticed a relationship between the combinatorial analysisa and Newton's binomials, what made the Pascal's triangle a great tool for the more practical development of a Newton binomial.

Read too: Briot-Ruffini device - method for dividing polynomials

Definition of Newton's binomial

We define as binomial thepolynomial which has two terms. In some applications in Mathematics and Physics, it is necessary to calculate powers of a binomial. To facilitate the process, Isaac Newton noticed important regularities that allow us to find the polynomial that results from the power of a binomial.

instagram story viewer

Isaac Newton was a physicist and mathematician and made great contributions to both areas.

For some cases, the calculation is quite simple: just perform the multiplication of the binomial by itself using the distributive property. Up to a potency of order 3, we develop without much effort, as they are the well-known notable products, but for higher powers, calculate from the multiplication of the term by itself no sometimes it's a lot of work.

Examples

Remember that every number raised to zero is equal to 1 and that every number raised to 1 is itself, which is also true for the binomials.

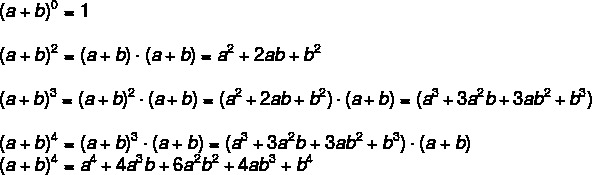
Newton noticed a relationship between the coefficients of each of the terms and the combination, which allowed the calculation of a power of a binomial more directly from the following formula:

Understanding the formula:

First let's look at the literal part of each term, which is the letter with its exponent. Note that, for each term, the exponent of “a” was decreasing, starting at n, then going to n – 1, and so on until it was 1 in the penultimate term and 0 in the last term (which makes the letter “a” not even appear in the last term).

**identifying The and its exponents:**

Now let's analyze the exponents of "b", which are always increasing, starting with 0 in the first term (the which makes the letter b not appear in the first term), 1 in the second term, and so on until it is equal The noin the last term.

identifying B and its exponents:

Understanding the literal part, let's analyze the coefficients, which are all combinations of no elements taken from 0 to 0, 1 to 1, 2 to 2, and so on until the last term, which is the combination of no elements taken from no in no.

It is noteworthy that it is important to master the calculation of combinations to be able to find the coefficients. Remember, to calculate combinations, we have to:

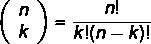
The combination response is always a natural number.

See too: Polynomial division: how to solve it?

Example: Calculate Newton's binomial (a+b) to the fourth power.

1st step: write the polynomial using the formula.

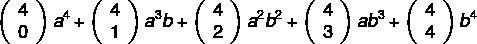
2nd step: calculate the combinations.

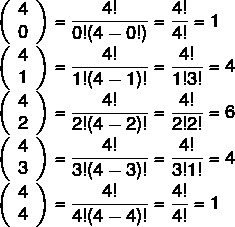
By replacing the combinations, the polynomial found will be:

You can see that solving cases like this is still laborious, depending on the exponent, but even so it is faster than calculating using the distributive property. A tool that can help with this calculation is Pascal's triangle.

Pascal's Triangle

The Pascal triangle was developed by Blaise Pascal during the study of combinations. He is a way that makes calculating combinations easier. Using the Pascal triangle makes it faster and easier to find the coefficients of the literal parts of a Newton binomial without having to calculate all the combinations.

To construct Pascal's triangle directly, let's remember two situations where the combination calculation is equal to 1.

Thus, the first and last term of all lines are always equal to 1. The central terms are built from the sum of the term above it plus its neighbor from the previous column, as in the representation below:

To build the next lines, just remember that the first term is 1 and the last one too. Then it is enough to do the sums to discover the central terms.

Also access: Polynomial Decomposition Theorem

Example: Calculate (a+b) to the sixth power.

1st step: apply the formula of the binomial.

2nd step: build Pascal's triangle to the 6th line.

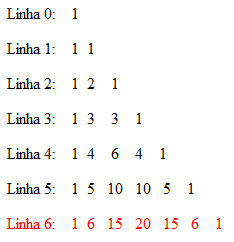
3rd step: replace the combinations with the values in line 6, which are the coefficients of each of the terms of the binomial.

What determines the number of lines we are going to build from the binomial is the value of n. It is important to remember that the first line is zero.

Construction of Pascal's triangle to the fifth line.

Newton's binomial general term

Newton's general term binomial is a formula that allows us to calculate a term of the binomial without having to develop the entire polynomial, that is, we can identify any of the terms from first to last. With the formula, we directly calculate the term we are looking for.

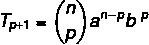
The: first term

B: second term

n: exponent

p+1: search term

Example: Find the 11th term of the binomial (a + b)¹².

Resolution:

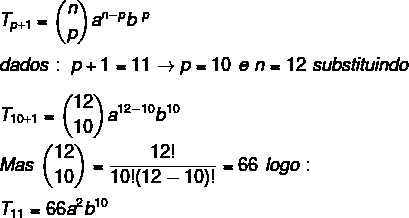
See too: Demonstrations through of algebraic calculus

solved exercises

Question 1 - (Cesgranrio) The coefficient of x⁴in the polynomial P(x) = (x + 2)⁶:

a) 64

b) 60

c) 12

d) 4

e) 24

Resolution

We want to find a specific term in solving the binomial; for that, we need to find the value of p.

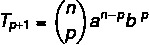
We know that the first term in this case is equal to x, so n – p = 4, as n = 6, we have:

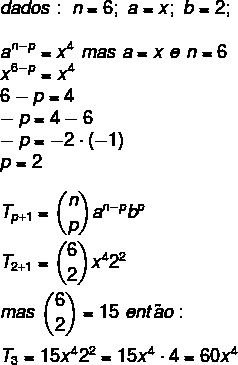
Hence, the coefficient is 60 (alternative B).

Question 2 - (Unifor) If the central term of the binomial development (4x + ky)¹⁰ for 8064x⁵y⁵, then the alternative that corresponds to the value of k will be:

a) 1/4

b) 1/2

c) 1

d) 2

e) 4

Resolution: We know that the central term has equal coefficients (p= 5). Let's find the 6th term, since p+1=6. Furthermore, we have that a = 4x; b = ky and n = 10, so: