determine the root of a role is to calculate the values of x that satisfy the 2nd degree equation ax² + bx + c = 0, which can be found through the Bhaskara's Theorem:
Number of real roots of 2nd degree function
Given the function f (x) = ax² + bx + c, there will be three cases to be considered to obtain the number of roots. This will depend on the value of the discriminant Δ.
1st case → Δ > 0: The function has two real and distinct roots, that is, different ones.
2nd case → Δ = 0: The function has real and equal roots. In this case, we say that the function has a single root.
3rd case → Δ < 0: The function has no real roots.
sum and product of roots
Let the equation be, ax² + bx + c = 0, we have that:
If Δ ≥ 0, the sum of the roots of this equation is given by 
and the product of the roots by 
. In fact, x’ and x’’ are the roots of the equation, so we have:
sum of roots
Root product
By carrying out the multiplication, we have:
Substituting Δ for b² – 4ac, we have:
After simplification, we have:
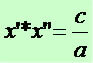
by Mark Noah
Graduated in Mathematics
High School Function - Roles - Math - Brazil School
Source: Brazil School - https://brasilescola.uol.com.br/matematica/raizes-funcao.htm