For a better understanding of the concept of exponential inequalities, it is important to know the concepts of exponential equations, if you haven't studied this concept yet, visit our article exponential equation.
In order to understand inequalities, we must know what is the main fact that differentiates them from equations. The main fact is regarding the sign of inequality and equality, when we work with equations we are looking for a value that equals another, on the other hand, in the inequality we will determine values that attest to that inequality.
However, the methods to proceed in the resolution are very similar, always seeking to determine an equality or inequality with elements with the same numerical base.
The crucial fact in algebraic expressions in this way is to have this inequality with the same numerical basis, because the unknown is found in the exponent and in order to be able to relate the exponents of the numbers there is a need for them to be in the same base numerical.
We will see some algebraic manipulations in some exercises that are recurrent in the resolutions of exercises involving exponential inequalities.
See the following question:
(PUC-SP) In the exponential function
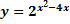
determine the values of x for which 1
We must determine this inequality by obtaining numbers on the same numerical basis.
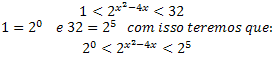
Since we now only have numbers in number base 2, we can write this inequality in relation to the exponents.
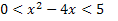
We must determine the values that satisfy the two inequalities. Let's make the left inequality first.
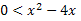
We must find the roots of the quadratic equation x2-4x=0 and compare the range of values with respect to inequality.
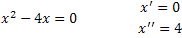
We must compare the inequality into three intervals, (the interval less than x’, the interval between x’ and x’’, and the interval greater than x’’).
For values less than x’’, we will have the following:
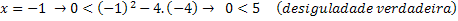
Therefore, values less than x = 0 satisfy this inequality. Let's look at values between 0 and 4.
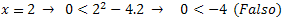
Therefore, it is not a valid range.
Now values greater than 4.
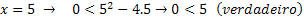
So for inequality:
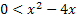
The solution is:
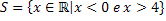
This inequality resolution can be done through the inequality of the second degree, obtaining the graph and determining the interval:
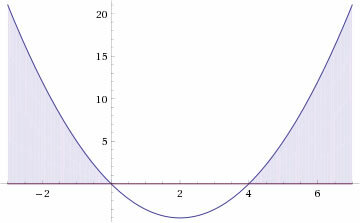
We must now determine the solution of the other inequality:
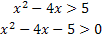
The roots are the same, we should just test the intervals. Testing the intervals will obtain the following solution set:
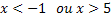
Using the graphic resource:
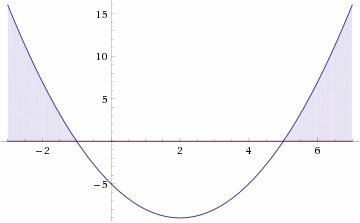
Therefore, to solve the two inequalities, we must find the interval that satisfies the two inequalities, that is, we just need to make the intersection of the two graphs.
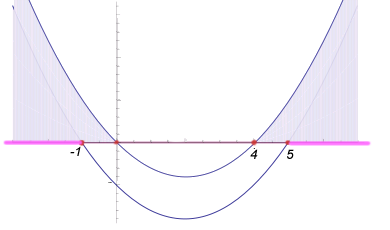
Thus, the solution set for the inequality
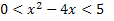
é:
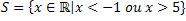
That is, these are the values that satisfy the exponential inequality:

Note that it took several concepts to realize just one inequality, so it is important to understand all of the algebraic procedures for transforming the base of a number, as well as finding the solution of inequalities of the first and second degree.
By Gabriel Alessandro de Oliveira
Graduated in Mathematics
Brazil School Team
Source: Brazil School - https://brasilescola.uol.com.br/matematica/inequacoes-exponenciais.htm

